（九）Transformer 模型，最牛皮的模型

Transformer 模型

• Transformer 是一种 Seq2Seq 模型
• Transformer 不是 RNN
• Transformer 只有 Attention 和 Dense 层
• Transformer 在 NLP 完爆其他模型

剥离 RNN，保留 Attention

Attention

Encoder 端的输入 $\bold x_1,\bold x_2,\dots,\bold x_m$，经过映射生成 $\bold k_{:i}$ 和 $\bold v_{:i}$

• Key: $\bold k_{:i}=\bold W_K \bold x_i$
• Value: $\bold v_{:i}=\bold W_V \bold x_i$

Decoder 端的输入 $\bold x_1',\bold x_2',\dots,\bold x_t'$，经过映射生成 $\bold q_{:j}$

• Query: $\bold q_{:i}=\bold W_Q \bold x_j'$

计算权重向量 $\bold{\alpha_{:i}}$：

$\bold{\alpha_{:i}}=Softmax(\bold K^T\bold{q_{:1}})$

计算上下文向量（Context Vector）：

$\bold c_{:1}=\bold{\alpha_{11}\bold{v_{:1}}}+\dots+\bold{\alpha_{m1}\bold{v_{:m}}}=\bold V \bold{\alpha_{:1}}$

直到所有 $\bold c$ 向量都计算完毕

$\bold c_{:j}=\bold{\alpha_{1j}\bold{v_{:1}}}+\dots+\bold{\alpha_{mj}\bold{v_{:m}}}=\bold V \bold{\alpha_{:j}}$

上面公式又可写作：

$\bold c_{:j}=\bold V \bold{\alpha_{:j}}=\bold V \cdot softmax(\bold K^T\bold q_{:j})=\bold V \cdot softmax(\bold {(\bold W_K \bold X)}^T\bold {\bold W_Q \bold x_j'})$

所以每个 $\bold c$ 向量都只和当前的 $\bold x_j'$ 与 所有的 $\bold x_i$ 相关。

这就是 Attention:

$\bold C=\text{Attn}(\bold X,\bold X')$

• Encoder 的输入：$\bold X=[\bold x_1,\bold x_2,\dots,\bold x_m]$
• Decoder 的输入：$\bold X'=[\bold x_1',\bold x_2',\dots,\bold x_t']$
• 参数矩阵：$\bold W_Q,\bold W_K,\bold W_V$

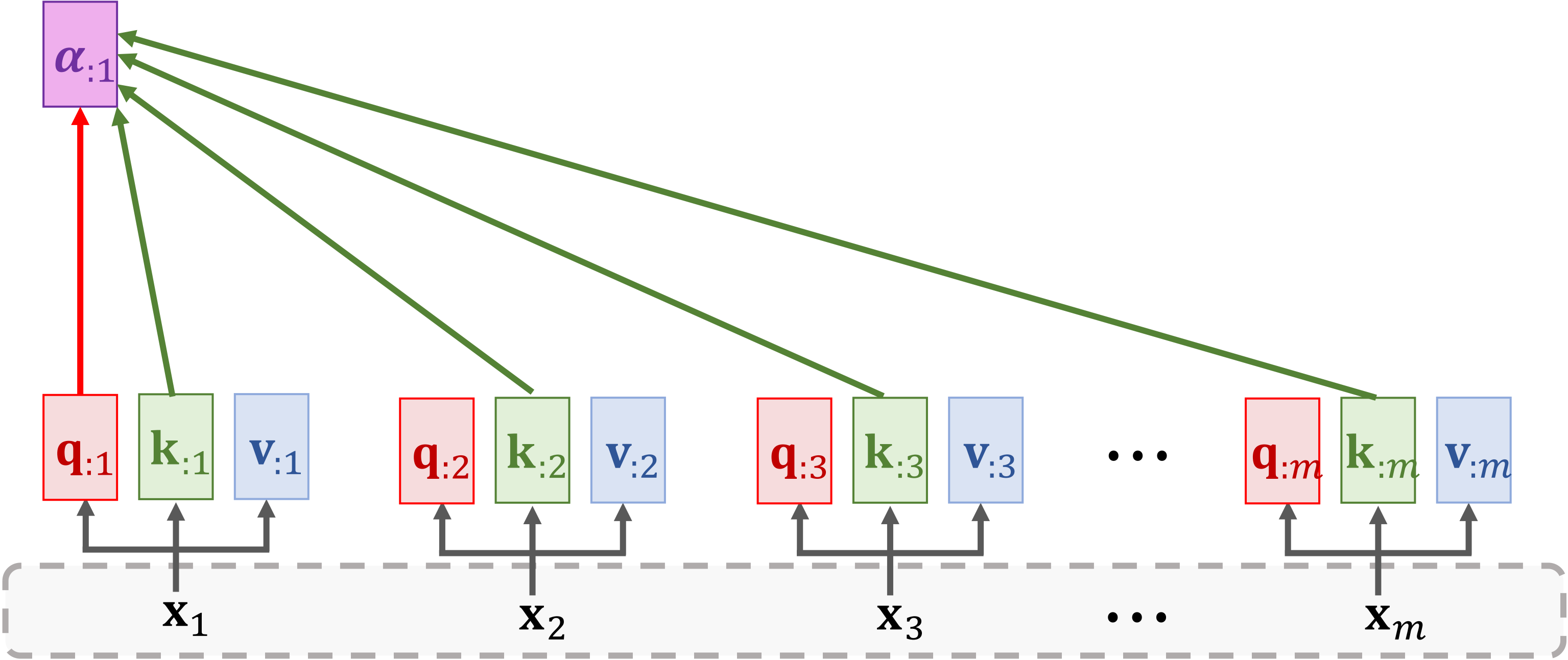
Self-Attention

对于 Self-Attention 来说，可用同一函数来处理，输入稍稍变一下即可

$\bold C=\text{Attn}(\bold X,\bold X)$

• 输入：$\bold X=[\bold x_1,\bold x_2,\dots,\bold x_m]$
• 参数矩阵：$\bold W_Q,\bold W_K,\bold W_V$

输入 $\bold x_1,\bold x_2,\dots,\bold x_m$，经过映射生成 $\bold q_{:i}$, $\bold k_{:i}$ 和 $\bold v_{:i}$

• Query: $\bold q_{:i}=\bold W_Q \bold x_i$
• Key: $\bold k_{:i}=\bold W_K \bold x_i$
• Value: $\bold v_{:i}=\bold W_V \bold x_i$

计算所有的 $\bold \alpha_{:j}$ 向量（$\bold \alpha_{1},\bold \alpha_{2},\dots,\bold \alpha_{m}$）

$\bold{\alpha_{:j}}=Softmax(\bold K^T\bold{q_{:j}})$

计算所有的 $\bold c_{:j}$ 向量（$\bold c_{1},\bold c_{2},\dots,\bold c_{m}$）

$\bold c_{:j}=\bold{\alpha_{1j}\bold{v_{:1}}}+\dots+\bold{\alpha_{mj}\bold{v_{:m}}}=\bold V \bold{\alpha_{:j}}$

所有的 $\bold c$ 向量就是 Self-Attention 的输出

上面公式又可写作：

$\bold c_{:j}=\bold V \bold{\alpha_{:j}}=\bold V \cdot softmax(\bold K^T\bold q_{:j})=\bold V \cdot softmax(\bold {(\bold W_K \bold X)}^T\bold {\bold W_Q \bold x_j})$

所以每个 $\bold c$ 向量都只和当前的 $\bold x_j$ 与 所有的 $\bold x_i$ 相关。

Multi-Head Self-Attention

单头自注意力可以被合并为多头自注意力，我愿称之为横向扩展

Stacked Self-Attention Layers

给每一个上下文向量后面都接一个 Dense 层，经过映射，再重新作为输入，接到到另一个 Self-Attention Layer。

我愿称之为纵向扩展。

Encoder

所以，以一个 Stacked Self-Attention Layers 作为 block。

6 个这样的 blocks 连在一起就叫做一个 Transformer 的 Encoder

Decoder

以前熟悉的 LSTM Encoder + Decoder （Seq2Seq）整体变成了一个 Decoder，叠了6 层的Encoder 输出的结果和目标文本经过多头 Self-Attention 的结果得到的上下文向量共同输入到多头 Attention 层，最终得到 $\bold z$ 向量，经过 Dense 层得到最终的输出 $\bold s$

这样一个结构叫做一个 Decoder 的 block

Transformer

将 6 个 Decoders 和 6 个 Encoders 连接在一起，就得到了一个 Transformer

总结

Encoder 总结：

• 1 encoder block ≈ multi-head self-attention + dense.
• Input shape: 512 × m.
• Output shape: 512 × m.
• Encoder network is a stack of 6 such blocks.

Decoder 总结：

• 1 decoder block ≈ multi-head self-attention + multi-head attention + dense.
• Input shape: (512 × m, 512 × t)
• Output shape: 512 × t.
• Decoder network is a stack of 6 such blocks.

Transformer 的完整实现