Spark 大数据入门清单：AHP法分析顾客终身价值得分

什么是 AHP 法

层次分析法（The analytic hierarchy process,简称AHP），也称层级分析法。

层次分析法的基本思路与人对一个复杂的决策问题的思维、判断过程大体上是一样的。比如：

1. 买钢笔，一般要依据质量、颜色、实用性、价格、外形等方面的因素选择某一支钢笔。
2. 假期旅游，是去风光秀丽的苏州，还是去迷人的北戴河，或者是去山水甲天下的桂林，那一般会依据景色、费用、食宿条件、旅途等因素来算着去哪个地方。

层次分析法是一种定性和定量相结合的、系统的、层次化的分析方法。这种方法的特点就是在对复杂决策问题的本质、影响因素及其内在关系等进行深入研究的基础上，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。是对难以完全定量的复杂系统做出决策的模型和方法。

层次分析法的基本步骤

1. 建立层次结构模型
2. 构造成对比较阵
3. 计算权向量并做一致性检验

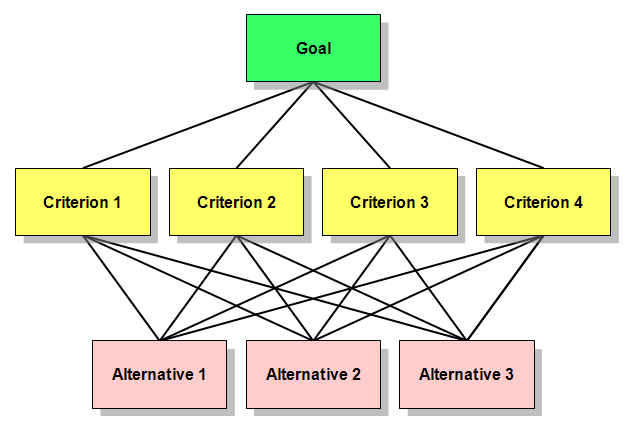
建立层次结构模型

将问题包含的因素分层：

1. 最高层(目标层)：决策的目的、要解决的问题；
2. 中间层(准则层或指标层)：考虑的因素、决策的准则；
3. 最低层(方案层)：决策时的备选方案；

我们的 Goal 是 ：RFM 同类用户排名

我们的 Criterions 是：R、F、M

我们的 Alternatives 是：每一个用户的 AHP 得分

构造成对比较矩阵

比较第 $i$ 个元素与第 $j$ 个元素相对上一层某个因素的重要性时，使用数量化的相对权重 $a_{ij}$来描述。设共有 $n$ 个元素参与比较，则 $A=(a_{ij})_{n\times n}$ 称为成对比较矩阵。

比较矩阵是一个方阵。

成对比较矩阵中 $a_{ij}$ 的取值可下述标度进行赋值。

• $a_{ij}=1$，元素 $i$ 与元素 $j$ 对上一层次因素的重要性相同；

• $a_{ij}=3$，元素 $i$ 比元素 $j$ 略重要；

• $a_{ij}=5$，元素 $i$ 比元素 $j$ 重要；

• $a_{ij}=7$，元素 $i$ 比元素 $j$ 重要得多；

• $a_{ij}=9$，元素 $i$ 比元素 $j$ 的极其重要；

• $a_{ji}=\frac{1}{a_{ij}}$

对于 RFM 的比较矩阵，我们假设如下：

$\begin{bmatrix} 1 & \frac{1}{5} & \frac{1}{7} \\\ 5 & 1 & \frac{1}{3} \\\ 7 & 3 & 1 \end{bmatrix}$

每行、每列分别代表 R、F、M。

$a_{21}=5$ 表示 F 比 R 为 5，即决策者认为 Frequency 比 Recency 重要。

import breeze.linalg._

// data 需要一列一列的输入
val rfmMatrix = DenseMatrix.create(rows = 3, cols = 3, data = Array(1, 5, 7, 1.0 / 5.0, 1, 3, 1.0 / 7.0, 1.0 / 3.0, 1))

计算权向量并做一致性检验

计算权向量

计算权向量的过程，大概分为 3 个步骤：(下面代码里面的m指的就是上文中提到的rfmMatrix)

1. 计算每一列的和

   import scala.collection.mutable
   
   val sums = mutable.ArrayBuffer.fill(m.cols)(0.0)
   m.foreachPair {
     case ((_, j), value) =>
       sums(j) += value
   }
   val sumList = sums.toArray

   	R	F	M
   R	$1$	$\frac{1}{5}$	$\frac{1}{7}$
   F	$5$	$1$	$\frac{1}{3}$
   M	$7$	$3$	$1$
   sum	13.0	4.2	1.4762

2. 将每一列的数据除以对应列的和

   val normalizedM = m.mapPairs {
     case ((_, j), value) => value / sumList(j)
   }

   	R	F	M
   R	$\frac{1}{13.0}$	$\frac{\frac{1}{5}}{4.2}$	$\frac{\frac{1}{7}}{1.4762}$
   F	$\frac{5}{13.0}$	$\frac{1}{4.2}$	$\frac{\frac{1}{3}}{1.4762}$
   M	$\frac{7}{13.0}$	$\frac{3}{4.2}$	$\frac{1}{1.4762}$

   运算的结果是：

   	R	F	M
   R	$0.0769$	$0.0476$	$0.0968$
   F	$0.3846$	$0.2381$	$0.2258$
   M	$0.5385$	$0.7143$	$0.6774$

3. 计算权向量：每一行数据的平均值

   val criteriaWeights = mutable.ArrayBuffer.fill(m.rows)(0.0)
   normalizedM.foreachPair {
     case ((i, _), value) => criteriaWeights(i) += value / m.rows.toDouble
   }
   val _criteriaWeights = criteriaWeights.toArray

   	R	F	M	criteria weights
   R	$0.0769$	$0.0476$	$0.0968$	$\frac{(0.0769+0.0476+0.0968)}{3}$
   F	$0.3846$	$0.2381$	$0.2258$	$\frac{(0.3846+0.2381+0.2258)}{3}$
   M	$0.5385$	$0.7143$	$0.6774$	$\frac{(0.5385+0.7143+0.6774)}{3}$

   运算的结果是：

   	R	F	M	criteria weights
   R	$0.0769$	$0.0476$	$0.0968$	$0.0738$
   F	$0.3846$	$0.2381$	$0.2258$	$0.2828$
   M	$0.5385$	$0.7143$	$0.6774$	$0.6434$

验证权向量的一致性

验证权向量的一致性，主要分为 5 个步骤：

1. 将原始矩阵拿去与权向量计算（相乘相加）

   val weightNormalizedM = m.mapPairs {
     case ((_, j), value) => value * _criteriaWeights(j)
   }

   	R	F	M
   R	$1\times{0.0738}$	$\frac{1}{5}\times{0.2828}$	$\frac{1}{7}\times{0.6434}$
   F	$5\times{0.0738}$	$1\times0.2828$	$\frac{1}{3}\times0.6434$
   M	$7\times{0.0738}$	$3\times0.2828$	$1\times0.6434$

   运算结果是：

   	R	F	M
   R	$0.0738$	$0.0566$	$0.0919$
   F	$0.3689$	$0.2828$	$0.2145$
   M	$0.5164$	$0.8485$	$0.6434$

2. 计算权重加和值（上一步中的结果，每行分别求和）

   val weightedSumValues = mutable.ArrayBuffer.fill(m.cols)(0.0d)
   weightNormalizedM.foreachPair {
     case ((i, _), value) => weightedSumValues(i) += value
   }

   	R	F	M	weighted sum values
   R	$0.0738$	$0.0566$	$0.0919$	0.2223
   F	$0.3689$	$0.2828$	$0.2145$	0.8662
   M	$0.5164$	$0.8485$	$0.6434$	2.0083

3. 计算 $\lambda_{max}$

   $\lambda_{max}= \frac{\sum_{i=1}^{n}{\frac{weightedSumValue_i} {\\\_criteriaWeight_i}}}{n} \\\ =\frac{\frac{weightedSumValue_1} {\\\_criteriaWeight_1}+\frac{weightedSumValue_2} {\\\_criteriaWeight_2}+\frac{weightedSumValue_3}{\\\_criteriaWeight_3}}{3}$

   val lambdaMax = (weightedSumValues.toArray / _criteriaWeights).sum / m.rows
   // 这里的/号是breeze.linalg.ImmutableNumericOps#/，可以让 Array 像 numpy 数组一样相除

   $\lambda_{max}=3.065511827120929$

4. 计算 CI（一致性指标，Consistency Index）

   $C.I.=\frac{\lambda_{max}}{n-1}$

   val CI = (lambdaMax - m.rows) / (m.rows - 1)

   $C.I.=0.03275591356046448$

5. 计算 CR（一致性比率，Consistency Ratio）

   判断方法如下： 当 CR < 0.1 时，判定成对比较阵具有满意的一致性，或其不一致程度是可以接受的；否则就调整成对比较矩阵，直到达到满意的一致性为止。

   $C.R.=\frac{C.I.}{R.I}$

   val CR = CI / getRI(m.rows)

   随机指标的值有表规定如下

   阶数	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
   R.I.	0	0	0.58	0.9	1.12	1.24	1.32	1.41	1.45	1.49	1.51	1.54	1.56	1.57	1.58

   写成代码如下：

   /**
   * 获取相应矩阵维度对应的 RI 值
   * @param n 矩阵的维度
   * @return RI 值
   */
   private def getRI(n: Int): Double = Map(1 -> 0.0, 2 -> 0.0,
     3 -> 0.58, 4 -> 0.90, 5 -> 1.12, 6 -> 1.24,
     7 -> 1.32, 8 -> 1.41, 9 -> 1.45, 10 -> 1.49)(n)

   $C.R.=0.056475713035283585 \lt 0.10$

   这说明不是一致阵，但具有满意的一致性，不一致程度是可接受的。

使用权向量

同属于一类的用户之间的排序，就靠权向量来解决，通过权向量给每个用户定下最终的分数：

设标准化的 R 为 $N_R$ ，标准化的 F 为 $N_F$，标准化的 M 为 $N_M$

设权向量分别为：$W_R$、$W_F$、$W_M$

即有：

$AHP_{score}=W_RN_R+W_FN_F+W_MN_M,(W_R=0.0738,W_F=0.2828,W_M=0.6434)$

1. 将 RFM 三值标准化

   val minmax = rfmWithLabelDF.agg(min("R"), min("F"), min("M"),
     max("R"), max("F"), max("M"))
   // 下面这些值可能是Long，如果报错的话请及时调整
   val minR = minmax.select("min(R)").head().getInt(0)
   val minF = minmax.select("min(F)").head().getInt(0) 
   val minM = minmax.select("min(M)").head().getInt(0)
   val maxR = minmax.select("max(R)").head().getInt(0)
   val maxF = minmax.select("max(F)").head().getInt(0)
   val maxM = minmax.select("max(M)").head().getInt(0)
   val udfNormalizeR = udf((r: Int) => {
     (maxR.toDouble - r.toDouble) / (maxR.toDouble - minR.toDouble)
   })
   val udfNormalizeF = udf((f: Int) => {
     (f.toDouble - minF.toDouble) / (maxF.toDouble - minF.toDouble)
   })
   val udfNormalizeM = udf((m: Int) => {
     (m.toDouble - minM.toDouble) / (maxM.toDouble - minM.toDouble)
   })
   val normalizedRFMDF = rfmWithLabelDF.withColumn("normalizedR", udfNormalizeR($"R"))
    .withColumn("normalizedF", udfNormalizeF($"F"))
    .withColumn("normalizedM", udfNormalizeM($"M"))

2. 计算 AHP 分数

   import org.apache.spark.sql.functions._
   import org.apache.spark.sql.expressions.Window
   
   val criteriaWeightsBC = spark.sparkContext.broadcast(criteriaWeights)
   
   val udfCalcAHPScore = udf((nR: Double, nF: Double, nM: Double) => {
     nR * criteriaWeightsBC.value(0) + nF * criteriaWeightsBC.value(1) + nM * criteriaWeightsBC.value(2)
   })
   
   val rfmWthLabelAndAHPScoreRankDF = normalizedRFMDF.withColumn("ahpScore", udfCalcAHPScore($"normalizedR", $"normalizedF", $"normalizedM"))
     // window function rank 将数据按照分区进行排序，详参 https://jaceklaskowski.gitbooks.io/mastering-spark-sql/spark-sql-functions-windows.html#rank
     .withColumn("rank", rank over Window.partitionBy("label").orderBy($"ahpScore".desc))
     .cache()

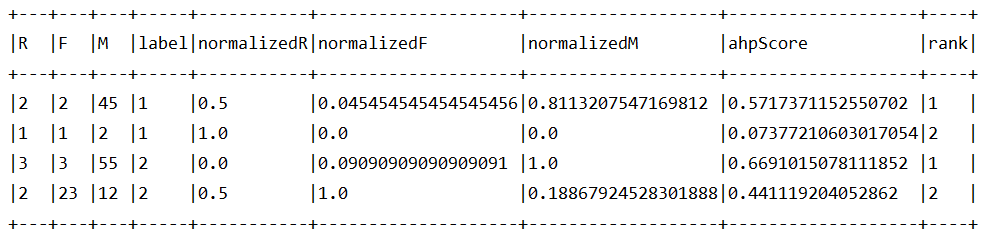
3. 展示、统计和保存

   rfmWthLabelAndAHPScoreRankDF.show(truncate = false, numRows = 200)
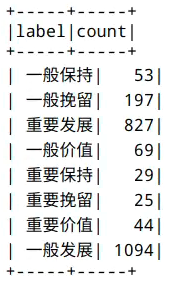
   rfmWthLabelAndAHPScoreRankDF.groupBy("label").count().show()
   rfmWthLabelAndAHPScoreRankDF.write
     .mode(SaveMode.Overwrite)
     .option("header", value = true)
     .csv("path/to/save")

总结

在进行客户分类后再对客户的类别进行顾客终身价值排序，使得企业能够量化各类客户的价值的差别，弥补了的客户分类方法的不足。这有助于企业制定更为可行的客户政策。由于受到成本的制约，电信企业不可能采取无差别的个性化服务，企业只能将资源集中在少数几类对企业重要的客户上。按照总得分的排列情况，企业应该优先将资源投放到总得分较高的客户身上。

参考文献