此篇学习笔记大多数为网络搬运+自己的理解,笔者学历不高,水平有限,就是给的多。此文所需的数学知识已经达到了笔者浅薄的认知极限。
Convex set
俗话定义:例如立方体、球体和圆形这样的没有凹痕和中空的集合就是凸集,月牙形不是凸集。
具体定义:在欧式空间中,凸集是对于集合内的每一对点,连接该对点的直线段上的每个点也都在该集合内。
抽象定义:凸集是在凸组合下闭合的仿射空间的子集。
数学定义:凸集,实数 R R R C C C S S S S S S S S S
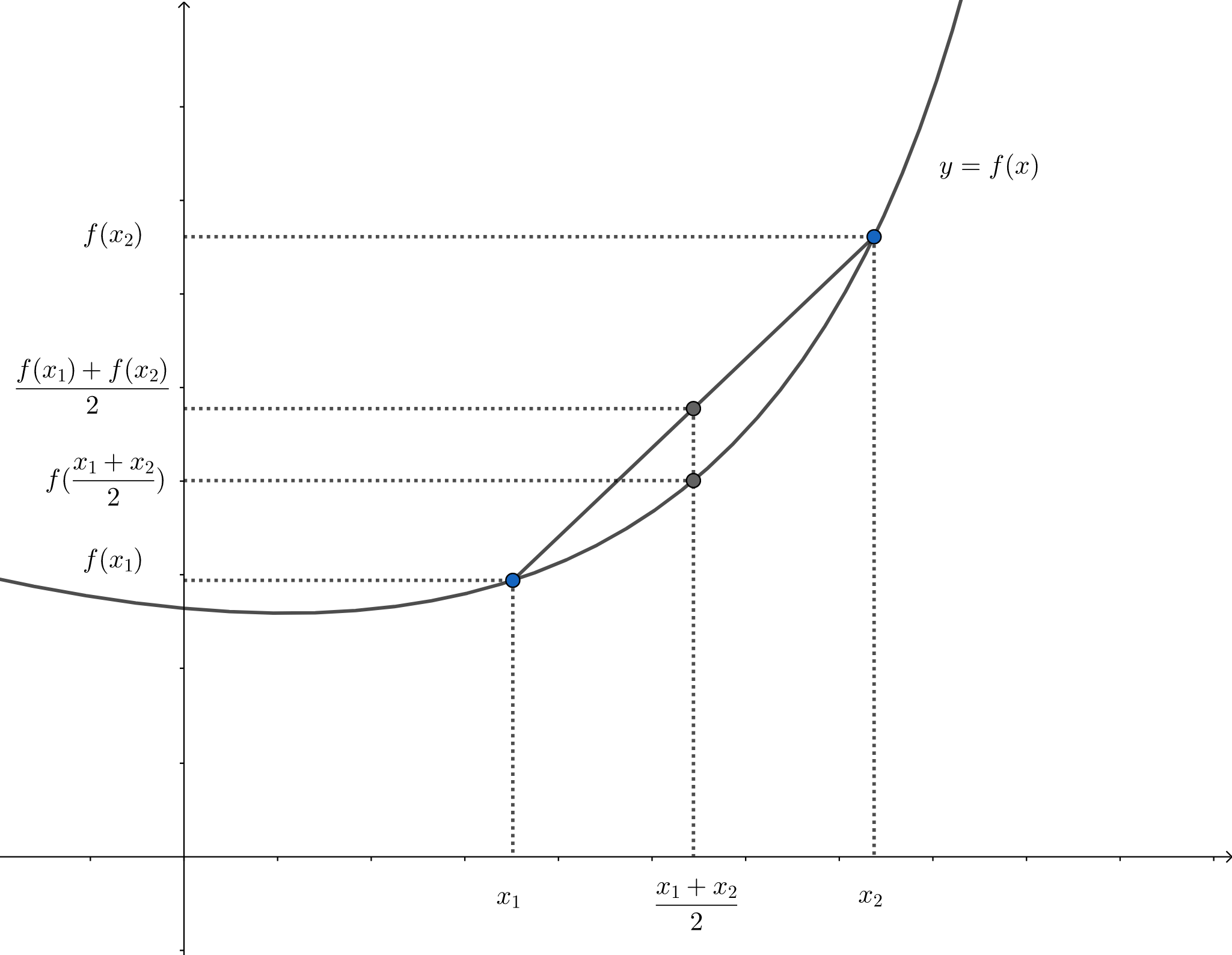
在区间上的凸函数
凸函数是指具有如下特性的一个定义在某个向量空间的凸子集 C C C f f f C C C x 1 x1 x 1 x 2 x2 x 2
f ( x 1 + x 2 2 ) ⩽ f ( x 1 ) + f ( x 2 ) 2 f(\frac{x_1+x_2}2)\leqslant\frac{f(x_1)+f(x_2)}2
f ( 2 x 1 + x 2 ) ⩽ 2 f ( x 1 ) + f ( x 2 )
对实数集上的函数,可通过求解二阶导数来判别:
若二阶导数在区间上非负,则称为凸函数
若二阶导数在区间上恒大于0,则称严格凸函数
线性规划(Linear Programming ,简称LP )为高中教材包含的内容,不再赘述,直接上例子唤醒回忆。
假设一个农夫有一块 A A A F F F P P P ( F 1 , P 1 ) (F_{1},P_{1}) ( F 1 , P 1 ) ( F 2 , P 2 ) (F_{2},P_{2}) ( F 2 , P 2 ) S 1 S_1 S 1 S 2 S_2 S 2
max Z S 1 x 1 + S 2 x 2 ( 最大化利润:目标函数 ) s . t . x 1 + x 2 ⩽ A ( 种植面积的限制 ) F 1 x 1 + F 2 x 2 ⩽ F ( 肥料数量的限制 ) P 1 x 1 + P 2 x 2 ⩽ P ( 农药数量的限制 ) x 1 ⩾ 0 , x 2 ⩾ 0 ( 不可以栽种负数的面积 ) \begin{matrix}
\begin{aligned}
\max Z &S_{1}x_{1}+S_{2}x_{2}&(\text{最大化利润:目标函数})\\
s.t. & x_1+x_2\leqslant A &(\text{种植面积的限制})\\
& F_1 x_1 + F_2 x_2 \leqslant F &(\text{肥料数量的限制})\\
& P_1 x_1 + P_2 x_2 \leqslant P & (\text{农药数量的限制})\\
& x_1 \geqslant 0,\, x_2 \geqslant 0 &(\text{不可以栽种负数的面积})\\
\end{aligned}
\end{matrix}
max Z s . t . S 1 x 1 + S 2 x 2 x 1 + x 2 ⩽ A F 1 x 1 + F 2 x 2 ⩽ F P 1 x 1 + P 2 x 2 ⩽ P x 1 ⩾ 0 , x 2 ⩾ 0 ( 最大化利润:目标函数 ) ( 种植面积的限制 ) ( 肥料数量的限制 ) ( 农药数量的限制 ) ( 不可以栽种负数的面积 )
几何上,线性约束条件的集合相当于一个凸包或凸集,叫做可行域。因为目标函数亦是线性的,所以其极值点会自动成为最值点。线性目标函数亦暗示其最优解只会出现在其可行域的边界点中。
是一种典型的优化问题,包括凸二次规划和非凸二次规划,在此类问题中,目标函数是变量的二次函数,约束条件是变量的线性不等式。
假定变量的个数为 d d d m m m
min x 1 2 x T Q x + c T x s . t . A x ⩽ b \begin{matrix}
\min_{x} &\frac{1}{2}x^TQx+c^Tx\\
s.t.&Ax \leqslant b
\end{matrix}
min x s . t . 2 1 x T Q x + c T x A x ⩽ b
其中 x x x d d d Q ∈ R d × d Q\in \mathbb{R^{d\times d }} Q ∈ R d × d A ∈ R m × d A\in \mathbb{R^{m \times d }} A ∈ R m × d b ∈ R m b\in \mathbb{R^m} b ∈ R m c ∈ R d c\in \mathbb{R^d} c ∈ R d A x ⩽ b Ax \leqslant b A x ⩽ b
若 Q Q Q
若 Q Q Q
若 Q Q Q
常用的二次规划问题求解方法有:
若 Q Q Q
正定矩阵是一种实对称矩阵。正定二次型 f ( x 1 , x 2 , … , x n ) = X T A X f(x_1,x_2,…,x_n)=X^TAX f ( x 1 , x 2 , … , x n ) = X T A X A A A A A A
当考虑矩阵的特征值时:
若所有特征值均不小于零,则称为半正定。
若所有特征值均大于零,则称为正定。
从几何的角度看的话:正定、半正定矩阵的直觉代表一个向量经过它的变化后的向量与其本身的夹角小于等于90度。
在支持向量机和最大熵模型中都会用到拉格朗日对偶性,主要为解决约束最优化问题,通过将原始问题转换为对偶问题求解。
先从最简单的求函数最小值开始说起:
min x ∈ R n f ( x ) \min_{\boldsymbol{x} \in \mathbf{R}^n}f(\boldsymbol{x})
x ∈ R n min f ( x )
求 f ( x ) f(x) f ( x ) x x x f ( x ) f(x) f ( x ) R n R^n R n f ( x ) f(x) f ( x )
min x ∈ R n f ( x ) \min_{\boldsymbol{x} \in \mathbf{R}^n}f(\boldsymbol{x})
x ∈ R n min f ( x )
s . t . c i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , k h j ( x ) = 0 , j = 1 , 2 , ⋯ , l \begin{aligned}\mathbb{s.t.}\quad &c_i(\boldsymbol{x}) \le 0,\quad i=1,2,\cdots,k\\&h_j(\boldsymbol{x})=0,\quad j=1,2,\cdots,l\end{aligned}
s . t . c i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , k h j ( x ) = 0 , j = 1 , 2 , ⋯ , l
其中 f ( x ) , c i ( x ) , h j ( x ) 在 R n f(x),c_i(x),h_j(x)在R^n f ( x ) , c i ( x ) , h j ( x ) 在 R n
此时我们直接求导是无法解决了,要是可以将约束条件转换为未知变量或许就可以找到答案了。
为了求解原始问题,我们首先引入广义拉格朗日函数 (generalized Lagrange function):
L ( x , α , β ) = f ( x ) + ∑ i = 1 k α i c i ( x ) + ∑ j = 1 l β j h j ( x ) L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta})=f(\boldsymbol{x})+\sum_{i=1}^k \alpha_ic_i(\boldsymbol{x}) + \sum_{j=1}^l\beta_jh_j(\boldsymbol{x})
L ( x , α , β ) = f ( x ) + i = 1 ∑ k α i c i ( x ) + j = 1 ∑ l β j h j ( x )
其中 x = ( x 1 , x 2 , ⋯ , x n ) T ∈ R n \boldsymbol{x}=(x_1,x_2,\cdots,x_n)^T \in \mathbf{R}^n x = ( x 1 , x 2 , ⋯ , x n ) T ∈ R n α i \alpha_i α i β j \beta _j β j α i ≥ 0 \alpha_i \ge 0 α i ≥ 0
拉格朗日函数虽然一眼看去十分复杂,但是其实它是将所有的限定条件加上新引入的变量(拉格朗日乘子)构成了一个新的函数,这样就将限定条件转换为了未知变量。
此时我们考虑 x x x
θ P ( x ) = max α , β : α i ≥ 0 L ( x , α , β ) \theta_P(\boldsymbol{x})=\max_{\boldsymbol{\alpha,\beta}:\alpha_i\ge0}L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta})
θ P ( x ) = α , β : α i ≥ 0 max L ( x , α , β )
下标 p 代表原始问题。
可以证明,如果 x x x θ ( x ) = f ( x ) \theta(\boldsymbol{x})=f(\boldsymbol{x}) θ ( x ) = f ( x )
如果 x x x c i ( x ) ≤ 0 ; h j ( x ) = 0 c_i(x)\le 0;h_j(x)=0 c i ( x ) ≤ 0 ; h j ( x ) = 0 θ ( x ) = + ∞ \theta(\boldsymbol{x})=+\infty θ ( x ) = + ∞
θ P ( x ) = { f ( x ) , x 满足原始问题约束 + ∞ , 其他 \theta_P(\boldsymbol{x})=\begin{cases}f(\boldsymbol{x}),&\boldsymbol{x} \text{满足原始问题约束}\\+\infty,&\text{其他}\end{cases} %]]>
θ P ( x ) = { f ( x ) , + ∞ , x 满足原始问题约束 其他
所以如果考虑极小化问题:
min x θ P ( x ) = min x max α , β : α i ≥ 0 L ( x , α , β ) \min_{\boldsymbol{x}}\theta_P(\boldsymbol{x})=\min_{\boldsymbol{x}}\max_{\boldsymbol{\alpha,\beta}:\alpha_i\ge0}L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta})
x min θ P ( x ) = x min α , β : α i ≥ 0 max L ( x , α , β )
就会发现它是与原始最优化问题等价的,即它们有相同的解。
min x max α , β : α i ≥ 0 L ( x , α , β ) \min_{\boldsymbol{x}}\max_{\boldsymbol{\alpha,\beta}:\alpha_i\ge0}L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta}) min x max α , β : α i ≥ 0 L ( x , α , β )
p ∗ = min x θ P ( x ) p^*=\min_{x}\theta_P(x)
p ∗ = x min θ P ( x )
总结一下原始问题和拉格朗日函数:从原始问题开始,通过拉格朗日函数重新定义一个无约束问题,这个无约束问题等价于原来的约束优化问题,从而将约束问题无约束化。也就是将d个变量和k个约束条件的最优化问题转换为d+k个变量的最优化问题。到此我们还是无法求解,我们需要将原始问题转换成对偶问题来求解。
我们再定义:
θ D ( α , β ) = min x L ( x , α , β ) \theta_D(\alpha,\beta)=\min_x L(x,\alpha,\beta)
θ D ( α , β ) = x min L ( x , α , β )
并极大化 θ D \theta_D θ D
max α , β θ D ( α , β ) = max α , β min x L ( x , α , β ) \max_{\alpha,\beta}\theta_D(\alpha,\beta)=\max_{\boldsymbol{\alpha,\beta}}\min_{\boldsymbol{x}}L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta})
α , β max θ D ( α , β ) = α , β max x min L ( x , α , β )
max α , β min x L ( x , α , β ) \max_{\boldsymbol{\alpha,\beta}}\min_{\boldsymbol{x}}L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta}) max α , β min x L ( x , α , β )
max α , β θ D ( α , β ) = max α , β min x L ( x , α , β ) s . t . α i ≥ 0 , i = 1 , 2 , ⋯ , k \begin{aligned}
\max_{\alpha,\beta}\theta_D(\alpha,\beta)= \max_{\boldsymbol{\alpha,\beta}}\min_{\boldsymbol{x}}L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta}) \\
\mathbb{s.t.}\quad\alpha_i\ge0,\quad i=1,2,\cdots,k
\end{aligned}
α , β max θ D ( α , β ) = α , β max x min L ( x , α , β ) s . t . α i ≥ 0 , i = 1 , 2 , ⋯ , k
我们将上面的问题称为原始问题的对偶问题。定义对偶问题的最优值
d ∗ = max α , β θ D ( α , β ) d^* = \max_{\alpha,\beta}\theta_D(\alpha,\beta)
d ∗ = α , β max θ D ( α , β )
对比原始问题,对偶问题是先固定 α α α β β β x x x α α α β β β
原始问题是先固定 x x x α α α β β β x x x
若原始问题和对偶问题都有最优值,那么
d ∗ = max α , β min x L ( x , α , β ) ≤ min x max α , β : α i ≥ 0 L ( x , α , β ) = p ∗ d^*=\max_{\boldsymbol{\alpha,\beta}}\min_{\boldsymbol{x}}L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta})\le\min_{\boldsymbol{x}}\max_{\boldsymbol{\alpha,\beta}:\alpha_i\ge0}L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta})=p^*
d ∗ = α , β max x min L ( x , α , β ) ≤ x min α , β : α i ≥ 0 max L ( x , α , β ) = p ∗
也就是说原始问题的最优值不小于对偶问题的最优值,但是我们要通过对偶问题来求解原始问题,就必须使得原始问题的最优值与对偶问题的最优值相等,于是可以得出下面的推论:
设 x ∗ x^∗ x ∗ α ∗ α^∗ α ∗ β ∗ β^∗ β ∗ d ∗ = p ∗ d^∗=p^∗ d ∗ = p ∗ x ∗ x^∗ x ∗ α ∗ α^∗ α ∗ β ∗ β^∗ β ∗
对偶问题跟原始问题可以看成本来是两个问题,因为优化的顺序不同而会得出两个不一定相关的值(但是 m i n x m a x y f ( x , y ) ≥ m a x y m a x x f ( x , y ) \mathop{min}_{x}\mathop{max}_{y}f(x,y) \geq \mathop{max}_{y}\mathop{max}_{x}f(x,y) min x ma x y f ( x , y ) ≥ ma x y ma x x f ( x , y )
两者的差值就是 duality gap,描述了我用另一种方式刻画问题的时候所造成的误差,强对偶的情况下最优值没有差别。
在最优点处将会满足KKT 条件,但是KKT条件本身并不需要问题满足强对偶。关于KKT条件什么时候不满足,有一种另外的理解是他要求各个函数的梯度张成足够大的空间(因为KKT的最后一条本质上是一个 A x = 0 Ax=0 A x = 0
所以,当原始问题和对偶问题的最优值相等:d ∗ = p ∗ d^∗ =p^* d ∗ = p ∗ d ∗ = p ∗ d^∗=p^∗ d ∗ = p ∗
若原始问题(对偶问题)有一个确定的最优解,那么对偶问题(原始问题)也有一个确定的最优解,而且这两个最优解所对应的目标函数值相等,这就是强对偶性。
对原始问题和对偶问题,假设函数 f ( x ) f(x) f ( x ) c i ( x ) c_i(x) c i ( x ) h j ( x ) h_j(x) h j ( x ) c i ( x ) c_i(x) c i ( x ) x ∗ x^∗ x ∗ α ∗ α^∗ α ∗ β ∗ β^∗ β ∗ x ∗ x^∗ x ∗ α ∗ α^∗ α ∗ β ∗ β^∗ β ∗
∇ x L ( x ∗ , α ∗ , β ∗ ) = 0 ∇ α L ( x ∗ , α ∗ , β ∗ ) = 0 ∇ β L ( x ∗ , α ∗ , β ∗ ) = 0 α i ∗ c i ( x ∗ ) = 0 , i = 1 , 2 , ⋯ , k c i ( x ∗ ) ≤ 0 , i = 1 , 2 , ⋯ , k α i ∗ ≥ 0 , i = 1 , 2 , ⋯ , k h j ( x ∗ ) = 0 , j = 1 , 2 , ⋯ , l \begin{aligned}
\nabla_\boldsymbol{x}L(\boldsymbol{x}^*,\boldsymbol{\alpha}^*,\boldsymbol{\beta}^*)=0 \\
\nabla_\boldsymbol{\alpha}L(\boldsymbol{x}^*,\boldsymbol{\alpha}^*,\boldsymbol{\beta}^*)=0 \\
\nabla_\boldsymbol{\beta}L(\boldsymbol{x}^*,\boldsymbol{\alpha}^*,\boldsymbol{\beta}^*)=0 \\
\alpha_i^*c_i(\boldsymbol{x}^*)=0,\quad i=1,2,\cdots,k\\
c_i(\boldsymbol{x}^*)\le0,\quad i=1,2,\cdots,k\\
\alpha_i^*\ge0,\quad i=1,2,\cdots,k\\
h_j(\boldsymbol{x}^*)=0,\quad j=1,2,\cdots,l
\end{aligned}
∇ x L ( x ∗ , α ∗ , β ∗ ) = 0 ∇ α L ( x ∗ , α ∗ , β ∗ ) = 0 ∇ β L ( x ∗ , α ∗ , β ∗ ) = 0 α i ∗ c i ( x ∗ ) = 0 , i = 1 , 2 , ⋯ , k c i ( x ∗ ) ≤ 0 , i = 1 , 2 , ⋯ , k α i ∗ ≥ 0 , i = 1 , 2 , ⋯ , k h j ( x ∗ ) = 0 , j = 1 , 2 , ⋯ , l
关于KKT 条件的理解:前面三个条件是对于各个变量的偏导数为0(这就解释了一开始为什么假设三个函数连续可微,如果不连续可微的话,这里的偏导数存不存在就不能保证),后面四个条件就是原始问题的约束条件以及拉格朗日乘子需要满足的约束。
f ( x ) = A x + b f(\boldsymbol{x})=\boldsymbol{A}\boldsymbol{x}+b
f ( x ) = A x + b
仿射函数就是一个线性函数,其输入是n维向量,参数 A可以是常数,也可以是m×n的矩阵,b可以是常数,也可以是m维的列向量,输出是一个m维的列向量。在几何上,仿射函数是一个线性空间到另一个线性空间的变换。
凸优化有个非常重要的定理,即任何局部最优解即为全局最优解。由于这个性质,只要设计一个较为简单的局部算法,例如贪婪算法(Greedy Algorithm)或梯度下降法(Gradient Decent),收敛求得的局部最优解即为全局最优。因此求解凸优化问题相对来说是比较高效的。这也是为什么机器学习中凸优化的模型非常多,毕竟机器学习处理大数据,需要高效的算法。
而非凸优化问题被认为是非常难求解的,因为可行域集合可能存在无数个局部最优点,通常求解全局最优的算法复杂度是指数级的(NP难)。最经典的算法要算蒙特卡罗投点法了,大概思想便是随便投个点,然后在附近区域(可以假设convex)得到局部最优值。然后随机再投个点,再找到局部最优点。如此反复,直到满足终止条件。
因为现实生活中,几乎所有问题的本质是非凸的。
科学的本质便是由简到难,先把简单问题研究透彻,然后把复杂问题简化为求解一个个简单问题。例如上面提到的投点法,就是在求解一个个的凸优化问题。假设需要求解 1w 个凸优化问题可以找到非凸优化的全局最优点,那么凸优化被研究透彻了,会加速凸优化问题的求解时间,例如0.001秒。这样求解非凸优化问题=求解1w个凸优化问题=10秒,还是可以接受的。
线性规划是运筹学最基础的课程,其可行域(可行解的集合)是多面体(polyhedron),具有着比普通的凸集更好的性质。因此是比较容易求解的(多项式时间可解)。
深度学习里的损失函数,是一个高度复合的函数。例如 h ( x ) = f ( g ( x ) ) h(x)=f(g(x)) h ( x ) = f ( g ( x ) ) f f f g g g
当 f f f g g g h h h h h h
求解这个非凸函数的最优解,类似于求凸优化中某点的梯度,然后按照梯度最陡的方向搜索。不同的是,复合函数无法求梯度,于是这里使用 Back Propagation 求解一个类似梯度的东西,反馈能量,然后更新。
深度学习中的优化问题,虽然目标函数非常复杂,但是它没有约束。运筹学由目标函数和约束条件组成,而约束条件,是使得运筹学的优化问题难以求解的重要因素。
P问题 :在多项式时间内可以被解决的问题NP问题 :在多项式时间内可以被验证其正确性的问题
售货员旅行问题 (traveling salesman problem),是最具有代表性的NP问题之一。假设一个推销员需要从香港出发,经过广州,北京,上海,…,等 n 个城市, 最后返回香港。 任意两个城市之间都有飞机直达,但票价不等。现在假设公司只给报销 C 块钱,问是否存在一个行程安排,使得他能遍历所有城市,而且总的路费小于 C?
推销员旅行问题显然是 NP 的。因为如果你任意给出一个行程安排,可以很容易算出旅行总开销。但是,要想知道一条总路费小于 C 的行程是否存在,在最坏情况下,必须检查所有可能的旅行安排! 这将是个天文数字。
这个天文数字到底有多大?目前的方法接近一个一个的排着试,还没有找到更好可以寻得最短路径的方法。对七个城而言,共有 6 ! = 720 6!=720 6 ! = 7 2 0 19 ! 19! 1 9 ! n ! n! n ! 1.21 × 1 0 17 1.21 \times 10^{17} 1 . 2 1 × 1 0 1 7 3.84 × 1 0 9 3.84 \times 10^9 3 . 8 4 × 1 0 9 3.15 × 1 0 7 3.15 \times 10^7 3 . 1 5 × 1 0 7
NPC(Non-deterministic Polynomial Complete) Problem : 满足两个条件 (1)是一个NP问题 (2) 所有的NP问题都可以约化到它NP-Hard Problem : 满足NPC问题的第二条,但不一定要满足第一条
NP困难(NP-hardness, non-deterministic polynomial-time hardness)问题是计算复杂性理论中最重要的复杂性类之一。如果所有NP问题都可以多项式时间归约到某个问题,则称该问题为NP困难。
因为NP困难问题未必可以在多项式时间内验证一个解的正确性(即不一定是NP问题),因此即使NP完全问题有多项式时间的解(P=NP),NP困难问题依然可能没有多项式时间的解。因此NP困难问题“至少与NP完全问题一样难”。
在数学中,0-1整数规划的线性规划的松弛 是这样的问题:把每个变量必须为0或1的约束,替换为较弱的每个变量属于区间[0,1]的约束。
也就是说,对于原整数规划的每个下列形式的约束:x ∈ { 0 , 1 } x \in \{0, 1\} x ∈ { 0 , 1 }
我们转而使用一对线性约束来代替:0 ≤ x i ≤ 1 0 \le x_i \le 1 0 ≤ x i ≤ 1
这样产生的松弛是线性规划,因此得名线性规划的松弛 。这种松弛技术把NP难的最优化问题(整数规划)转化为一个相关的多项式时间可解的问题(线性规划)。我们可以用松弛后的线性规划的解来获得关于原整数规划的解的信息。
拉格朗日松弛技术是一个非常简单而漂亮地转化方法。
首先,拉格朗日松弛技术是用在优化问题里面(假设是最小化问题),而且一定是有约束条件的优化问题。
假设我们已经知道没有约束条件的优化问题怎么解了。然后对于有约束条件的优化问题,我们想懒一点的话,就可以想想办法怎么把它转化成没有约束条件的优化问题。
于是有人就想到
直接去掉约束条件
那显然定义域变大了,那得到的最小值肯定不比原来的大。那怎么办?
那就如果不满足某些约束条件,我们就来点惩罚
这个惩罚表现在目标函数上。我们在目标函数上多加一项,如果某些约束条件没有满足,那目标函数就会变大。
另外我们也多了拉格朗日乘子,它也是我们可以动的变量。这时候最优的结果当然会满足所有约束条件,不然就被罚惨了。
这就是所谓的拉格朗日松弛技术,是把有约束优化问题转化成无约束优化问题的好方法。
我们知道拉格朗日乘子法在保留原函数的基础上引入了一个线性项,那么这个线性项有什么作用呢?它保证了在获得最优乘子的情况下,原目标函数的解和拉格朗日函数的解是一致的。具体是怎么做的呢?
我们假设当前点偏离了等式约束,并且我们已知偏离等式约束的这个点对应的原函数的值要比满足等式约束值的原函数的最优值要小。那么拉格朗日引入了这个线性项之后,两者相加,大于那个最优值。那么这样实际上最优值还是在等式约束满足的情况下得到。
因此拉格朗日函数就起到了对偏离等式约束的惩罚作用,保证了原目标函数和拉格朗日函数解的一致性。
虽然说拉格朗日乘子法的线性项只是对原目标函数的一个线性逼近,也就是说两者之间不是等价的,但是拉格朗日乘子法,能够保证在取得最优乘子的情况下两者解的一致性,那么很显然通过求解拉格朗日函数的最优解来求得原目标函数的最优解是一种更实际,更方便的做法。
比如要解如下问题:
min x 2 + y 2 s . t . x + y = 1 \begin{aligned}
\min x^2+y^2\\
s.t.\space \space \space x+y=1
\end{aligned}
min x 2 + y 2 s . t . x + y = 1
我们可以用拉格朗日乘子 p p p
min L ( x , y , p ) = x 2 + y 2 + p ( 1 − x − y ) \min L(x,y,p)=x^2+y^2+p(1-x-y)
min L ( x , y , p ) = x 2 + y 2 + p ( 1 − x − y )
令:∂ L ∂ x = 0 , ∂ L ∂ y = 0 \frac{\partial L}{\partial x}=0,\frac{\partial L}{\partial y}=0 ∂ x ∂ L = 0 , ∂ y ∂ L = 0
可得:x = y = p 2 x=y=\frac{p}2 x = y = 2 p
又∵ x + y = 1 \because x+y=1 ∵ x + y = 1
∴ x = y = 0.5 , p = 1 \therefore x=y=0.5,p=1 ∴ x = y = 0 . 5 , p = 1
p p p
连续优化(continuous optimization)
连续优化是求解在连续变量的问题,其一般地是求一组实数,或者一个函数。
离散优化(discrete optimization)
连续优化是求解离散变量的问题,是从一个无限集或者可数无限集里寻找一个对象,典型地是一个整数,一个集合,一个排列,或者一个图。
组合优化(combinatorial optimization)
组合优化问题的目标是从组合问题的可行解集中求出最优解,通常可描述为:令 Ω = { s 1 , s 2 , … , s n } Ω=\{s1,s2,…,sn\} Ω = { s 1 , s 2 , … , s n } C ( s i ) C(s_i) C ( s i ) s i s_i s i s s s s i ∈ Ω s_i \in Ω s i ∈ Ω C ( s ∗ ) = min C ( s i ) C(s^*)=\min C(s_i) C ( s ∗ ) = min C ( s i )
典型的组合优化问题有旅行商问题、加工调度问题、0-1背包问题、装箱问题、图着色问题、聚类问题等。这些问题描述非常简单,并且有很强的工程代表性,但最优化求解很困难,其主要原因是求解这些问题的算法需要极长的运行时间与极大的存储空间,以致根本不可能在现有计算机上实现,即所谓的“组合爆炸”。正是这些问题的代表性和复杂性激起了人们对组合优化理论与算法的研究兴趣。
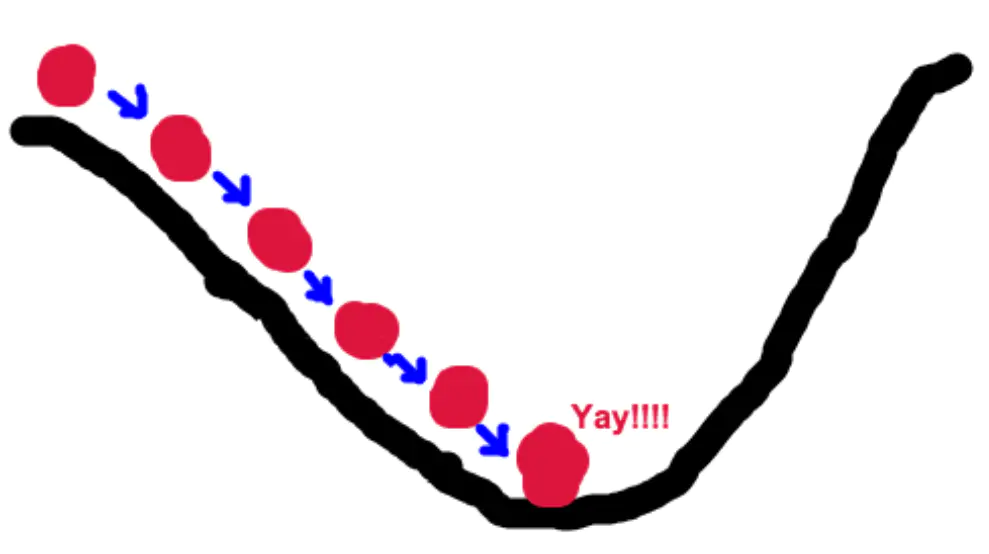
梯度下降法的基本思想可以类比为下山的过程。假设这样一个场景:一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
单变量函数的微分:
f ( x ) = x 2 f ′ ( x ) = 2 x \begin{aligned}
f(x)=x^2 \\
f'(x)=2x
\end{aligned}
f ( x ) = x 2 f ′ ( x ) = 2 x
多变量函数的微分:
f ( x , y ) = x 2 y 2 ∂ f ∂ x = 2 x y 2 , ∂ f ∂ y = x 2 2 y \begin{aligned}
f(x,y)=x^2y^2\\
\frac{\partial{f}}{\partial{x}}=2xy^2,\frac{\partial{f}}{\partial{y}}=x^22y
\end{aligned}
f ( x , y ) = x 2 y 2 ∂ x ∂ f = 2 x y 2 , ∂ y ∂ f = x 2 2 y
以上这些内容都很好理解,单变量函数微分对那一个变量求导数即可,多变量函数微分,对每一个变量求偏导数即可。
而后者,就是梯度。
假设有:
J ( θ ) = 0.55 − ( 5 θ 1 + 2 θ 2 − 12 θ 3 ) J(\theta)=0.55-(5\theta_1+2\theta_2-12\theta_3)
J ( θ ) = 0 . 5 5 − ( 5 θ 1 + 2 θ 2 − 1 2 θ 3 )
所以其梯度可写作如下:
∇ J ( θ ) = ⟨ ∂ J ∂ θ 1 , ∂ J ∂ θ 2 , ∂ J ∂ θ 3 ⟩ = ⟨ − 5 , − 2 , 12 ⟩ \nabla{J(\theta)}=\lang{\frac{\partial{J}}{\partial{\theta_1}},\frac{\partial{J}}{\partial{\theta_2}},\frac{\partial{J}}{\partial{\theta_3}}}\rang=\lang{-5,-2,12}\rang
∇ J ( θ ) = ⟨ ∂ θ 1 ∂ J , ∂ θ 2 ∂ J , ∂ θ 3 ∂ J ⟩ = ⟨ − 5 , − 2 , 1 2 ⟩
我们可以看到,梯度就是分别对每个变量进行微分,然后用逗号分割开,梯度是用<>包括起来,说明梯度其实是向量。
在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率
在多变量函数中,梯度是向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向
我们需要到达山底,就需要在每一步观测到此时最陡峭的地方,梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,这正是我们所需要的。所以我们只要沿着梯度的方向一直走,就能走到局部的最低点。
梯度下降公式:
Θ 1 = Θ 0 − α ∇ J ( Θ ) \Theta^1=\Theta^0-\alpha{\nabla{J(\Theta)}}
Θ 1 = Θ 0 − α ∇ J ( Θ )
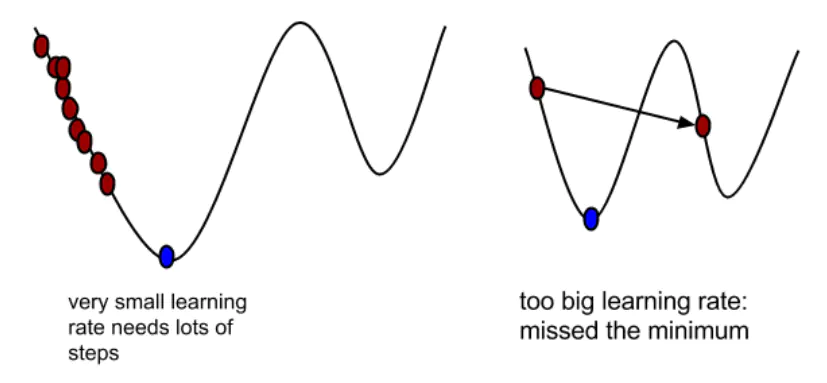
此公式是一个程序算法迭代的公式,等式右边的计算结果会赋值到等式左边。我们当前所处的位置为 Θ 0 \Theta^0 Θ 0 J J J α \alpha α Θ 1 \Theta^1 Θ 1
α \alpha α ( 0 , 1 ] (0,1] ( 0 , 1 ] α \alpha α
假设有单变量的函数:
J ( θ ) = θ 2 J(\theta)=\theta^2
J ( θ ) = θ 2
其微分:
J ′ ( θ ) = 2 θ J'(\theta)=2\theta
J ′ ( θ ) = 2 θ
随便选取初始点 θ 0 = 1 , α = 0.4 \theta^0=1,\alpha=0.4 θ 0 = 1 , α = 0 . 4 Θ 1 = Θ 0 − α ∇ J ( Θ ) \Theta^1=\Theta^0-\alpha{\nabla{J(\Theta)}} Θ 1 = Θ 0 − α ∇ J ( Θ )
θ 0 = 1 θ 1 = θ 0 − α × J ′ ( θ 0 ) = 1 − 0.4 × 2 = 0.2 θ 2 = θ 1 − α × J ′ ( θ 1 ) = 0.04 θ 3 = 0.008 θ 4 = 0.0016 \begin{aligned}
\theta^0&=1\\
\theta^1&=\theta^0-\alpha\times{J'(\theta^0)}\\
&=1-0.4\times{2}\\
&=0.2\\
\theta^2&=\theta^1-\alpha\times{J'(\theta^1)}\\
&=0.04\\
\theta^3&=0.008\\
\theta^4&=0.0016
\end{aligned}
θ 0 θ 1 θ 2 θ 3 θ 4 = 1 = θ 0 − α × J ′ ( θ 0 ) = 1 − 0 . 4 × 2 = 0 . 2 = θ 1 − α × J ′ ( θ 1 ) = 0 . 0 4 = 0 . 0 0 8 = 0 . 0 0 1 6
在上一篇种我们讨论了,「以当前的所处的位置为基准,寻找这个位置最陡峭的地方」,实际上在机器学习种,使用大量样本来学习时,就会导致样本集中的每一个样本都要计算一下梯度,损失函数的维度越高,计算所花费的时间成本就越高。
比如有如下损失函数,目标函数的损失函数通常取各个样本损失函数的平均:
J ( x ) = 1 n ∑ i = 1 n J ( x i ) J(x)=\frac{1}{n}\sum_{i=1}^{n}{J(x_i)}
J ( x ) = n 1 i = 1 ∑ n J ( x i )
其中 J ( x i ) J(x_i) J ( x i ) x i x_i x i x x x
∇ J ( x ) = 1 n ∇ ∑ i = 1 n J ( x i ) \nabla{J(x)}=\frac{1}{n}\nabla\sum_{i=1}^{n}{J(x_i)}
∇ J ( x ) = n 1 ∇ i = 1 ∑ n J ( x i )
如果使用梯度下降法(批量梯度下降法),那么每次迭代过程中都要对 n n n J ( x i ) J(x_i) J ( x i ) O ( n ) O(n) O ( n ) O ( 1 ) O(1) O ( 1 )
随机梯度下降的缺点:
选择合适的 learning rate 比较困难 - 对所有的参数更新使用同样的 learning rate。对于稀疏数据或者特征,有时我们可能想更新快一些对于不经常出现的特征,对于常出现的特征更新慢一些,这时候SGD就不太能满足要求了
SGD容易收敛到局部最优,并且在某些情况下可能被困在鞍点。
为了解决以上确定,引入下面两个主题。
如果说随机梯度下降或小批量随机梯度下降的收敛情况如下图:
那么,加上动量,让他震荡不那么极端的剧烈,就是类似下图的收敛情况:
上文中曾经提到过 Θ n = Θ n − 1 − α ∇ J ( Θ n ) \Theta_n=\Theta_{n-1}-\alpha{\nabla{J(\Theta_n)}} Θ n = Θ n − 1 − α ∇ J ( Θ n )
m n = γ m n − 1 + α ∇ J ( Θ n ) Θ n = Θ n − 1 − m n \begin{aligned}
m_n&=\gamma{m_{n-1}}+\alpha{\nabla{J(\Theta_n)}}\\
\Theta_n&=\Theta_{n-1}-m_n
\end{aligned}
m n Θ n = γ m n − 1 + α ∇ J ( Θ n ) = Θ n − 1 − m n
其中,n n n n − 1 n-1 n − 1 γ γ γ 0 ≤ γ < 1 0≤γ<1 0 ≤ γ < 1 γ = 0 γ=0 γ = 0
在超参数设置合适的情况下,还能达到更加好的在竖直方向上的移动更加平滑,且在水平方向上更快逼近最优解 的收敛效果:
假设当前时间步 t t t y t y_t y t t − 1 t−1 t − 1 y t − 1 y_{t−1} y t − 1 x t x_t x t
y t = γ y t − 1 + ( 1 − γ ) x t . y_t = \gamma y_{t-1} + (1-\gamma) x_t.
y t = γ y t − 1 + ( 1 − γ ) x t .
展开可得无穷级数形式:
y t = ( 1 − γ ) x t + γ y t − 1 = ( 1 − γ ) x t + ( 1 − γ ) ⋅ γ x t − 1 + γ 2 y t − 2 = ( 1 − γ ) x t + ( 1 − γ ) ⋅ γ x t − 1 + ( 1 − γ ) ⋅ γ 2 x t − 2 + γ 3 y t − 3 … \begin{aligned}
y_t &= (1-\gamma) x_t + \gamma y_{t-1}\\
&= (1-\gamma)x_t + (1-\gamma) \cdot \gamma x_{t-1} + \gamma^2y_{t-2}\\
&= (1-\gamma)x_t + (1-\gamma) \cdot \gamma x_{t-1} + (1-\gamma) \cdot \gamma^2x_{t-2} + \gamma^3y_{t-3}\\
&\ldots
\end{aligned}
y t = ( 1 − γ ) x t + γ y t − 1 = ( 1 − γ ) x t + ( 1 − γ ) ⋅ γ x t − 1 + γ 2 y t − 2 = ( 1 − γ ) x t + ( 1 − γ ) ⋅ γ x t − 1 + ( 1 − γ ) ⋅ γ 2 x t − 2 + γ 3 y t − 3 …
其中重复出现的部分是:( 1 − γ ) × γ n x t − n (1-\gamma)\times{\gamma^{n}x_{t-n}} ( 1 − γ ) × γ n x t − n
其中最重要的部分 γ n \gamma^n γ n γ \gamma γ ( 0 , 1 ] (0,1] ( 0 , 1 ] γ n \gamma^n γ n e x p ( − 1 ) ≈ 0.3679 exp(-1)\approx 0.3679 e x p ( − 1 ) ≈ 0 . 3 6 7 9
而
lim n → ∞ ( 1 − 1 n ) n = exp ( − 1 ) ≈ 0.3679 \lim_{n \rightarrow \infty} \left(1-\frac{1}{n}\right)^n = \exp(-1) \approx 0.3679
n → ∞ lim ( 1 − n 1 ) n = exp ( − 1 ) ≈ 0 . 3 6 7 9
所以,当 γ → 1 \gamma \rightarrow 1 γ → 1 γ 1 / ( 1 − γ ) = exp ( − 1 ) \gamma^{1/(1-\gamma)}=\exp(-1) γ 1 / ( 1 − γ ) = exp ( − 1 )
所以,上面的 γ n \gamma^n γ n n n n 1 1 − γ \frac{1}{1-\gamma} 1 − γ 1
比如,γ = 0.95 \gamma =0.95 γ = 0 . 9 5 y t ≈ 0.05 ∑ i = 0 19 0.9 5 i x t − i y_t \approx 0.05 \sum_{i=0}^{19} 0.95^i x_{t-i} y t ≈ 0 . 0 5 ∑ i = 0 1 9 0 . 9 5 i x t − i y t y_t y t x t x_t x t γ = 0.9 γ=0.9 γ = 0 . 9 y t y_t y t x t x_t x t t t t x t x_t x t
当自变量 x 1 x_1 x 1 x 2 x_2 x 2
由此引入下一个话题,它根据自变量在每个维度的梯度值的大小来调整各个维度上的学习率,从而避免统一的学习率难以适应所有维度的问题。
AdaGrad 算法会使用一个小批量随机梯度 g t \boldsymbol{g}_t g t s t \boldsymbol{s}_t s t s 0 \boldsymbol{s}_0 s 0 t t t g t \boldsymbol{g}_t g t s t \boldsymbol{s}_t s t ⊙ \odot ⊙
s t = s t − 1 + g t ⊙ g t , Θ t = Θ t − 1 − α s t + ϵ ⊙ g t \begin{aligned}
\boldsymbol{s_t}&=\boldsymbol{s}_{t-1}+\boldsymbol{g}_t \odot \boldsymbol{g}_t,\\
\Theta_t&=\Theta_{t-1}-\frac{\alpha}{\sqrt{\boldsymbol{s}_t + \epsilon}} \odot \boldsymbol{g}_t
\end{aligned}
s t Θ t = s t − 1 + g t ⊙ g t , = Θ t − 1 − s t + ϵ α ⊙ g t
其中 α \alpha α ϵ \epsilon ϵ 1 0 − 6 10^{−6} 1 0 − 6
需要强调的是,小批量随机梯度按元素平方的累加变量 s t \boldsymbol{s}_t s t s t \boldsymbol{s}_t s t
自变量的迭代轨迹较平滑,在迭代后期的移动幅度较小
s t = γ s t − 1 + ( 1 − γ ) g t ⊙ g t , Θ t = Θ t − 1 − α s t + ϵ ⊙ g t \begin{aligned}
\boldsymbol{s_t}&=\gamma\boldsymbol{s}_{t-1}+(1-\gamma)\boldsymbol{g}_t \odot \boldsymbol{g}_t,\\
\Theta_t&=\Theta_{t-1}-\frac{\alpha}{\sqrt{\boldsymbol{s}_t + \epsilon}} \odot \boldsymbol{g}_t
\end{aligned}
s t Θ t = γ s t − 1 + ( 1 − γ ) g t ⊙ g t , = Θ t − 1 − s t + ϵ α ⊙ g t
动量法和AdaGrad的结合,同样的学习率下,RMSProp 算法可以更快逼近最优解。
Adam 算法使用了动量变量 v t \boldsymbol{v}_t v t s t \boldsymbol{s}_t s t 0 ≤ β 1 < 1 0 \leq \beta_1 < 1 0 ≤ β 1 < 1 t t t v t \boldsymbol{v}_t v t g t \boldsymbol{g}_t g t
v t ← β 1 v t − 1 + ( 1 − β 1 ) g t . \boldsymbol{v}_t \leftarrow \beta_1 \boldsymbol{v}_{t-1} + (1 - \beta_1) \boldsymbol{g}_t.
v t ← β 1 v t − 1 + ( 1 − β 1 ) g t .
和 RMSProp 算法中一样,给定超参数 0 ≤ β 2 < 1 0 \leq \beta_2 < 1 0 ≤ β 2 < 1 g t ⊙ g t \boldsymbol{g}_t \odot \boldsymbol{g}_t g t ⊙ g t s t \boldsymbol{s}_t s t
s t ← β 2 s t − 1 + ( 1 − β 2 ) g t ⊙ g t . \boldsymbol{s}_t \leftarrow \beta_2 \boldsymbol{s}_{t-1} + (1 - \beta_2) \boldsymbol{g}_t \odot \boldsymbol{g}_t.
s t ← β 2 s t − 1 + ( 1 − β 2 ) g t ⊙ g t .
由于我们将 v 0 \boldsymbol{v}_0 v 0 s 0 \boldsymbol{s}_0 s 0 t t t v t = ( 1 − β 1 ) ∑ i = 1 t β 1 t − i g i \boldsymbol{v}_t = (1-\beta_1) \sum_{i=1}^t \beta_1^{t-i} \boldsymbol{g}_i v t = ( 1 − β 1 ) ∑ i = 1 t β 1 t − i g i ( 1 − β 1 ) ∑ i = 1 t β 1 t − i = 1 − β 1 t (1-\beta_1) \sum_{i=1}^t \beta_1^{t-i} = 1 - \beta_1^t ( 1 − β 1 ) ∑ i = 1 t β 1 t − i = 1 − β 1 t t t t β 1 = 0.9 \beta_1 = 0.9 β 1 = 0 . 9 v 1 = 0.1 g 1 \boldsymbol{v}_1 = 0.1\boldsymbol{g}_1 v 1 = 0 . 1 g 1 t t t v t \boldsymbol{v}_t v t 1 − β 1 t 1 - \beta_1^t 1 − β 1 t v t 和 s t \boldsymbol{v}_t和\boldsymbol{s}_t v t 和 s t
v ^ t ← v t 1 − β 1 t , s ^ t ← s t 1 − β 2 t . \hat{\boldsymbol{v}}_t \leftarrow \frac{\boldsymbol{v}_t}{1 - \beta_1^t},
\hat{\boldsymbol{s}}_t \leftarrow \frac{\boldsymbol{s}_t}{1 - \beta_2^t}.
v ^ t ← 1 − β 1 t v t , s ^ t ← 1 − β 2 t s t .
接下来,Adam算法使用以上偏差修正后的变量 v ^ t \hat{\boldsymbol{v}}_t v ^ t s ^ t \hat{\boldsymbol{s}}_t s ^ t
g t ′ ← η v ^ t s ^ t + ϵ , \boldsymbol{g}_t' \leftarrow \frac{\eta \hat{\boldsymbol{v}}_t}{\sqrt{\hat{\boldsymbol{s}}_t} + \epsilon},
g t ′ ← s ^ t + ϵ η v ^ t ,
其中 η \eta η ϵ \epsilon ϵ 1 0 − 8 10^{-8} 1 0 − 8 g t ′ \boldsymbol{g}_t' g t ′
x t ← x t − 1 − g t ′ . \boldsymbol{x}_t \leftarrow \boldsymbol{x}_{t-1} - \boldsymbol{g}_t'.
x t ← x t − 1 − g t ′ .
Adam 算法是 RMSProp 算法与动量法的结合。
首先,L-BFGS 算法是一种拟牛顿法,是求解非线性优化问题最有效的方法之一。
考虑如下无约束的极小化问题:
m i n x f ( x ) , min_\mathbf{x}f(\mathbf x),
m i n x f ( x ) ,
其中 x = ( x 1 , x 2 , … , x N ) T ∈ R N \mathbf x=(x_1,x_2,\dots,x_N)^T \in \mathbb{R}^N x = ( x 1 , x 2 , … , x N ) T ∈ R N f f f x ∗ x^* x ∗
首先考虑 N = 1 N=1 N = 1 f ( x ) f(\mathbf x) f ( x ) f ( x ) f(x) f ( x ) f ( x ) f(x) f ( x )
设 x k x_k x k
φ ( x ) = f ( x k ) + f ′ ( x k ) ( x − x k ) + 1 2 f ′ ′ ( x k ) ( x − x k ) 2 \varphi(x)=f(x_k)+f'(x_k)(x-x_k)+\frac{1}{2}f''(x_k)(x-x_k)^2
φ ( x ) = f ( x k ) + f ′ ( x k ) ( x − x k ) + 2 1 f ′ ′ ( x k ) ( x − x k ) 2
表示 f ( x ) f(x) f ( x ) x k x_k x k φ ( x ) \varphi(x) φ ( x )
φ ′ ( x ) = 0 , \varphi'(x)=0,
φ ′ ( x ) = 0 ,
即
f ′ ( x k ) + f ′ ′ ( x k ) ( x − x k ) = 0 , f'(x_k)+f''(x_k)(x-x_k)=0,
f ′ ( x k ) + f ′ ′ ( x k ) ( x − x k ) = 0 ,
从而得
x = x k − f ′ ( x k ) f ′ ′ ( x k ) , x=x_k-\frac{f'(x_k)}{f''(x_k)},
x = x k − f ′ ′ ( x k ) f ′ ( x k ) ,
于是,若给定初始值 x 0 x_0 x 0
x k + 1 = x k − f ′ ( x k ) f ′ ′ ( x k ) , k = 0 , 1 , … x_{k+1}=x_k-\frac{f'(x_k)}{f''(x_k)},k=0,1,\dots
x k + 1 = x k − f ′ ′ ( x k ) f ′ ( x k ) , k = 0 , 1 , …
产生序列 { x k } \{x_k\} { x k } f ( x ) f(x) f ( x ) { x k } \{x_k\} { x k } f ( x ) f(x) f ( x )
对于 N > 1 N > 1 N > 1
φ ( x ) = f ( x k ) + ∇ f ( x k ) ( x − x k ) + 1 2 ( x − x k ) T ∇ 2 f ( x k ) ( x − x k ) \varphi(\mathbf x)=f(\mathbf{x}_k)+\nabla f(\mathbf{x}_k)(\mathbf{x}-\mathbf{x}_k)+\frac{1}{2}(\mathbf{x}-\mathbf{x}_k)^T\nabla^2 f(\mathbf{x}_k)(\mathbf{x}-\mathbf{x}_k)
φ ( x ) = f ( x k ) + ∇ f ( x k ) ( x − x k ) + 2 1 ( x − x k ) T ∇ 2 f ( x k ) ( x − x k )
其中, ∇ f \nabla f ∇ f f f f ∇ 2 f \nabla^2f ∇ 2 f f f f
∇ f = [ ∂ f ∂ x 1 ∂ f ∂ x 2 ⋮ ∂ f ∂ x N ] , ∇ 2 f = [ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ∂ x 1 ∂ x N ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ⋯ ∂ 2 f ∂ x 2 ∂ x N ⋱ ∂ 2 f ∂ x N ∂ x 1 ∂ 2 f ∂ x N ∂ x 2 ⋯ ∂ 2 f ∂ x N 2 ] N × N \begin{aligned}
\nabla f=\left[\begin{array}{c}
\frac{\partial f}{\partial x_{1}} \\
\frac{\partial f}{\partial x_{2}} \\
\vdots \\
\frac{\partial f}{\partial x_{N}}
\end{array}\right], \quad \nabla^{2} f=\left[\begin{array}{cccc}
\frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{N}} \\
\frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{N}} \\
& & \ddots & \\
\frac{\partial^{2} f}{\partial x_{N} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{N} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{N}^{2}}
\end{array}\right]_{N \times N}
\end{aligned}
∇ f = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ ∂ x 1 ∂ f ∂ x 2 ∂ f ⋮ ∂ x N ∂ f ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ , ∇ 2 f = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ ∂ x 1 2 ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x N ∂ x 1 ∂ 2 f ∂ x 1 ∂ x 2 ∂ 2 f ∂ x 2 2 ∂ 2 f ∂ x N ∂ x 2 ∂ 2 f ⋯ ⋯ ⋱ ⋯ ∂ x 1 ∂ x N ∂ 2 f ∂ x 2 ∂ x N ∂ 2 f ∂ x N 2 ∂ 2 f ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ N × N
后续的方法和 N = 1 N=1 N = 1
设 g \mathbf{g} g ∇ f \nabla f ∇ f H H H ∇ 2 f \nabla^2f ∇ 2 f x 0 \mathbf{x}_0 x 0
x k + 1 = x k − H k − 1 g k , k = 0 , 1 , … \mathbf{x_{k+1}}=\mathbf{x}_k-H_k^{-1}\mathbf{g}_k,k=0,1,\dots
x k + 1 = x k − H k − 1 g k , k = 0 , 1 , …
这就是原始的牛顿迭代法,其迭代公式中的搜索方向 d k = − H k − 1 g k d_k=-H_k^{-1}\mathbf{g}_k d k = − H k − 1 g k
当目标函数是二次函数时,由于二次泰勒展开函数与原目标函数不是近似而是完全相同的二次式,海森矩阵退化成一个常数矩阵,从任一初始点出发,利用迭代公式只需一步迭代即可达到 f ( x ) f(x) f ( x ) x ∗ x^* x ∗ 二次收敛性 的算法。对于非二次函数,若函数的二次性态较强,或迭代点已经进入极小点的邻域,则其收敛速度也是很快的,这是牛顿法的主要优点。
但原始牛顿法由于迭代公式中没有步长因子,对于非二次型目标函数,有时会使函数值上升,即出现 f ( x k + 1 ) > f ( x k ) f(\mathbf{x}_{k+1}) > f(\mathbf{x}_{k}) f ( x k + 1 ) > f ( x k )
牛顿法是梯度下降法的进一步发展,梯度法利用目标函数的一阶偏导数信息、以负梯度方向作为搜索方向,只考虑目标函数在迭代点的局部性质;而牛顿法不仅使用目标函数的一阶偏导数,还进一步利用了目标函数的二阶偏导数,这样就考虑了梯度变化的趋势,因而能更全面的确定合适的搜索方向以加快收敛,它具有二阶收敛速度。但是存在以下两个确定:
对目标函数有严格的要求,函数必须是具有连续的一阶、二阶偏导数,海森矩阵必须正定,
计算复杂,除计算梯度外,还需要计算二阶偏导数矩阵和逆矩阵。
上节提到了牛顿法的缺点,拟牛顿法就是将牛顿法中用来计算搜索方向的海森矩阵做了近似计算。
设 B ≈ H , D ≈ H − 1 B \approx H, D\approx H^{-1} B ≈ H , D ≈ H − 1
设经过 k + 1 k+1 k + 1 x k + 1 \mathbf{x}_{k+1} x k + 1 f ( x ) f(x) f ( x ) x k + 1 \mathbf{x}_{k+1} x k + 1
f ( x ) ≈ f ( x k + 1 ) + ∇ f ( x k + 1 ) ⋅ ( x − x k + 1 ) + 1 2 ⋅ ( x − x k + 1 ) T ⋅ ∇ 2 f ( x k + 1 ) ⋅ ( x − x k + 1 ) f(\mathbf{x}) \approx f\left(\mathbf{x}_{k+1}\right)+\nabla f\left(\mathbf{x}_{k+1}\right) \cdot\left(\mathbf{x}-\mathbf{x}_{k+1}\right)+\frac{1}{2} \cdot\left(\mathbf{x}-\mathbf{x}_{k+1}\right)^{T} \cdot \nabla^{2} f\left(\mathbf{x}_{k+1}\right) \cdot\left(\mathbf{x}-\mathbf{x}_{k+1}\right)
f ( x ) ≈ f ( x k + 1 ) + ∇ f ( x k + 1 ) ⋅ ( x − x k + 1 ) + 2 1 ⋅ ( x − x k + 1 ) T ⋅ ∇ 2 f ( x k + 1 ) ⋅ ( x − x k + 1 )
两边同时求梯度,得
∇ f ( x ) ≈ ∇ f ( x k + 1 ) + H k + 1 ⋅ ( x − x k + 1 ) \nabla f(\mathbf{x}) \approx \nabla f\left(\mathbf{x}_{k+1}\right)+H_{k+1} \cdot\left(\mathbf{x}-\mathbf{x}_{k+1}\right)
∇ f ( x ) ≈ ∇ f ( x k + 1 ) + H k + 1 ⋅ ( x − x k + 1 )
取 x = x k \mathbf{x}=\mathbf{x}_k x = x k
g k + 1 − g k ≈ H k + 1 ⋅ ( x k + 1 − x k ) \mathrm{g}_{k+1}-\mathrm{g}_{k} \approx H_{k+1} \cdot\left(\mathrm{x}_{k+1}-\mathrm{x}_{k}\right)
g k + 1 − g k ≈ H k + 1 ⋅ ( x k + 1 − x k )
引入记号
s k = x k + 1 − x k , y k = g k + 1 − g k \mathbf{s}_{k}=\mathbf{x}_{k+1}-\mathbf{x}_{k}, \mathbf{y}_{k}=\mathbf{g}_{k+1}-\mathbf{g}_{k}
s k = x k + 1 − x k , y k = g k + 1 − g k
则
y k ≈ H k + 1 ⋅ s k \mathbf{y}_{k} \approx H_{k+1} \cdot \mathbf{s}_{k}
y k ≈ H k + 1 ⋅ s k
或
s k ≈ H k + 1 − 1 ⋅ y k \mathbf{s}_{k} \approx H_{k+1}^{-1} \cdot \mathbf{y}_{k}
s k ≈ H k + 1 − 1 ⋅ y k
这就是拟牛顿条件 ,它对迭代过程中的海森矩阵 H k + 1 H_{k+1} H k + 1 H k + 1 H_{k+1} H k + 1 B k + 1 B_{k+1} B k + 1 H k + 1 − 1 H_{k+1}^{-1} H k + 1 − 1 D k + 1 D_{k+1} D k + 1
y k = B k + 1 ⋅ s k \mathbf{y}_{k}=B_{k+1} \cdot \mathbf{s}_{k}
y k = B k + 1 ⋅ s k
或
s k = D k + 1 ⋅ y k \mathbf{s}_{k}=D_{k+1} \cdot \mathbf{y}_{k}
s k = D k + 1 ⋅ y k
由此条件,可以推导出DFP 算法 、BFGS 算法 ,其过程比较复杂,略去不讲,这两种算法是服从上述拟牛顿条件 的表述,但是其内存占用依然很高,需要用到 N × N N\times{N} N × N D k D_k D k N N N
所以提出 L-BFGS 算法,其基本思想是:不再存储完整的矩阵 D k D_k D k { s i } , { y i } \left\{s_{i}\right\},\left\{\mathbf{y}_{i}\right\} { s i } , { y i } D k D_k D k { s i } , { y i } \left\{s_{i}\right\},\left\{\mathbf{y}_{i}\right\} { s i } , { y i } { s i } , { y i } \left\{s_{i}\right\},\left\{\mathbf{y}_{i}\right\} { s i } , { y i } m m m O ( N 2 ) O(N^2) O ( N 2 ) O ( m N ) O(mN) O ( m N )
上一章说到了无约束非线性优化问题最有效的方法,牛顿法衍生出来的L-BFGS,那么关于约束问题最优化方法在机器学习中比较广泛使用的算法是 ADMM(交换方向乘子法)。
假设如下优化问题
m i n x f ( x ) s . t . A x = b \begin{aligned}
min_xf(x)\\
s.t.Ax=b
\end{aligned}
m i n x f ( x ) s . t . A x = b
ADMM通常解决的是等式约束的优化问题。
对偶方法:把minimize问题 f ( x ) f(x) f ( x ) A x = b Ax=b A x = b λ \lambda λ
L ( x , λ ) = f ( x ) + λ T ( A x − b ) L(x, \lambda)=f(x)+\lambda^{T}(A x-b)
L ( x , λ ) = f ( x ) + λ T ( A x − b )
原来带约束求解 m i n x f ( x ) min_xf(x) m i n x f ( x ) max λ min x L ( x , λ ) \max _{\lambda} \min _{x} L(x, \lambda) max λ min x L ( x , λ )
对偶上升法
step1: x k + 1 = arg min x L ( x , λ k ) step2: λ k + 1 = λ k + ρ ( A x k + 1 − b ) \begin{array}{ll}
\text {step1:} & x^{k+1}=\arg \min _{x} L\left(x, \lambda^{k}\right) \\
\text {step2:} & \lambda^{k+1}=\lambda^{k}+\rho\left(A x^{k+1}-b\right)
\end{array}
step1: step2: x k + 1 = arg min x L ( x , λ k ) λ k + 1 = λ k + ρ ( A x k + 1 − b )
实际上很好理解,就是把 max λ min x L ( x , λ ) \max _{\lambda} \min _{x} L(x, \lambda) max λ min x L ( x , λ ) max λ ( min x L ( x , λ ) ) \max _{\lambda} (\min _{x} L(x, \lambda)) max λ ( min x L ( x , λ ) )
对约束增加一个惩罚项,变成增广拉格朗日函数
L ( x , λ ) = f ( x ) + λ T ( A x − b ) + ρ 2 ∥ A x − b ∥ 2 L(x, \lambda)=f(x)+\lambda^{T}(A x-b)+\frac{\rho}{2}\|A x-b\|^{2}
L ( x , λ ) = f ( x ) + λ T ( A x − b ) + 2 ρ ∥ A x − b ∥ 2
下面是两个变量的增广拉格朗日函数:
L ( x , z , λ ) = f ( x ) + g ( z ) + λ T ( A x + B z − c ) + ρ 2 ∥ A x + B z − c ∥ 2 L(x, z, \lambda)=f(x)+g(z)+\lambda^{T}(A x+B z-c)+\frac{\rho}{2}\|A x+B z-c\|^{2}
L ( x , z , λ ) = f ( x ) + g ( z ) + λ T ( A x + B z − c ) + 2 ρ ∥ A x + B z − c ∥ 2
ADMM 流程就像对偶上升法一样分别固定另外两个变量,更新其中一个变量:(也就是其名:交替方向)
step1: x k + 1 = arg min x L ( x , z k , λ k ) step2: z k + 1 = arg min z L ( x k + 1 , z , λ k ) step3: λ k + 1 = λ k + ρ ( A x k + 1 + B z k + 1 − c ) \begin{aligned}
&\text {step1:} & x^{k+1}&=\arg \min _{x} L(x, z^{k}, \lambda^{k}) \\
&\text {step2:} & z^{k+1}&=\arg \min _{z} L(x^{k+1}, z, \lambda^{k}) \\
&\text {step3:}& \lambda^{k+1}&=\lambda^{k}+\rho(A x^{k+1}+B z^{k+1}-c)
\end{aligned}
step1: step2: step3: x k + 1 z k + 1 λ k + 1 = arg x min L ( x , z k , λ k ) = arg z min L ( x k + 1 , z , λ k ) = λ k + ρ ( A x k + 1 + B z k + 1 − c )
step1~3是大循环,求解里面的 arg min L \arg\min L arg min L






Preview: