规范化
上篇中我们提到了向量的方向性,其实向量除了方向还有大小。
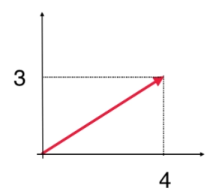
u=(3,4),问 u 的大小是多少?

在二维平面中,我们可以根据勾股定理得,u 的大小 ∥u∥=32+42=5,其中 ∥u∥ 也叫向量的模。
之所以模定义为双竖线,是与二范数相对应,所谓二范数就是平方开根号,三范数就是立方开根号,其中二范数的形式与欧拉距离是一样的。
再举个例子:
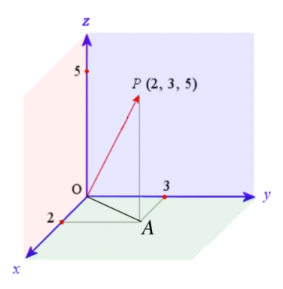
u=OP=(2,3,5)
u 的大小是多少?

∥OA∥=22+32
∥OP∥=∥OA∥2+∥AP∥2=22+32+52
∥u∥=22+32+52
同理,n 维度向量:
u=(u1,u2,…,un)T
∥u∥=u12+u22+…+un2
单位向量
模长为 1 ,长度不再重要,只表示方向。
假设有 u:
u=(u1,u2,…,un)T
其单位向量:
u^=∥u∥1⋅u=(∥u∥u1,∥u∥u2,…,∥u∥un)
∥u^∥=1 只表示方向

根据 u 求出 u^ 的过程,叫做归一化、规范化(normalize)
单位向量有无数个。

坐标轴上以 1 为半径的圆上的点都是单位向量。
其中,指向坐标轴正方向的,叫做标准单位向量。

蓝色为标准单位向量
在二维空间中,有两个标准单位向量:
e1=(1,0)e2=(0,1)
在三维空间中,有三个标准单位向量:
e1=(1,0,0)e2=(0,1,0)e3=(0,0,1)
在 n 维空间中,有 n 个标准单位向量:
e1=(1,0,…,0)e2=(0,1,…,0)…en=(0,0,…,1)
向量的模和单位向量的实现:
__init__.py
PYTHON from ._globals import EPSILON
|
_globals.py
Vector.py
PYTHON import math
from ._globals import EPSILON
class Vector:
def __init__(self, lst):
self._values = list(lst)
@classmethod
def zero(cls, dim):
"""返回一个dim维的零向量"""
return cls([0] * dim)
def __add__(self, another):
"""向量加法,返回结果向量"""
assert len(self) == len(another), \
"Error in adding. Length of vectors must be same."
return Vector([a + b for a, b in zip(self, another)])
def __sub__(self, another):
"""向量减法,返回结果向量"""
assert len(self) == len(another), \
"Error in subtracting. Length of vectors must be same."
return Vector([a - b for a, b in zip(self, another)])
def norm(self):
"""返回向量的模"""
return math.sqrt(sum(e**2 for e in self))
def normalize(self):
"""返回向量的单位向量"""
if self.norm() < EPSILON:
raise ZeroDivisionError("Normalize error! norm is zero.")
return Vector(self._values) / self.norm()
def __mul__(self, k):
"""返回数量乘法的结果向量:self * k"""
return Vector([k * e for e in self])
def __rmul__(self, k):
"""返回数量乘法的结果向量:k * self"""
return self * k
def __truediv__(self, k):
"""返回数量除法的结果向量:self / k"""
return (1 / k) * self
def __pos__(self):
"""返回向量取正的结果向量"""
return 1 * self
def __neg__(self):
"""返回向量取负的结果向量"""
return -1 * self
def __iter__(self):
"""返回向量的迭代器"""
return self._values.__iter__()
def __getitem__(self, index):
"""取向量的第index个元素"""
return self._values[index]
def __len__(self):
"""返回向量长度(有多少个元素)"""
return len(self._values)
def __repr__(self):
return "Vector({})".format(self._values)
def __str__(self):
return "({})".format(", ".join(str(e) for e in self._values))
|
向量的点乘与几何意义
向量点乘的定义
前面我们学习了向量的加法和数量相乘,说到向量的点乘,可能会让人直观的想是不是这样的乘法:
u⋅v=⎝⎜⎜⎛u1u2⋯un⎠⎟⎟⎞⋅⎝⎜⎜⎛v1v2⋯vn⎠⎟⎟⎞=⎝⎜⎜⎛u1⋅v1u2⋅v2⋯un⋅vn⎠⎟⎟⎞
向量中的元素分别相乘,但这是错误的,我们后面会讲到在几何中的理解就更容易理解了。
正确的两个向量相乘的方法是:
u⋅v=⎝⎜⎜⎛u1u2⋯un⎠⎟⎟⎞⋅⎝⎜⎜⎛v1v2⋯vn⎠⎟⎟⎞=sum⎝⎜⎜⎛u1⋅v1u2⋅v2⋯un⋅vn⎠⎟⎟⎞=u1⋅v1+u2⋅v2+⋯+un⋅vn
和错误的相比就多了一步,相乘的结果要相加。
两个向量相乘后的结果是一个数(标量),而不再是一个向量。
向量的点乘(dot product)又叫内积(inner product)。
在这一小结中给出这样的定义,后续再做解释。
点乘的几何意义
在几何上,
u⋅v==⎝⎜⎜⎛u1u2⋯un⎠⎟⎟⎞⋅⎝⎜⎜⎛v1v2⋯vn⎠⎟⎟⎞=u1⋅v1+u2⋅v2+⋯+un⋅vn∥u∥⋅∥v∥⋅cosθ
向量相乘的结果得到的标量恰好是两个向量模的乘积再乘以夹角的余弦值。
证明:
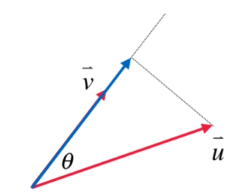
在二维空间中:

有 u 和 v,绿色箭头是 u−v ,其中 u−v 可以理解成 u+(−v),同一个箭头方向,同一个箭头大小,平移到上图所示即可。
∥u−v∥2=∥u∥2+∥v∥2−2⋅∥u∥⋅∥v∥⋅cosθ
移项之后:
∥u∥⋅∥v∥⋅cosθ=21(∥u∥2+∥v∥2−∥u−v∥2)=21(x12+y12+x22+y22−(x1−x2)2−(y1−y2)2)=21(x12+y12+x22+y22−x12+2x1x2−x22−y12+2y1y2−y22)=x1x2+y1y2
即证。
向量点乘的直观理解
上一节我们得出了下面向量点乘的公式:
u⋅v=∥u∥⋅∥v∥⋅cosθ
将它做一个小小的变形:
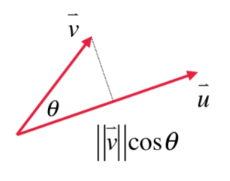
u⋅v=(∥u∥⋅cosθ)⋅∥v∥

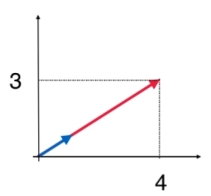
就可以把 ∥u∥⋅cosθ 看做 u 在 v 方向上的投影,也就是蓝色线。
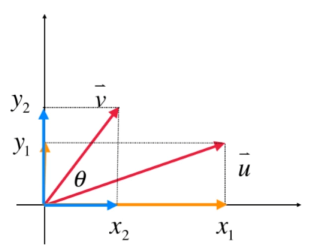
当然,也可以将 u 和 v 都投影到 x 轴和 y 轴上:

同方向的数值相乘,不同方向的乘积相加,就是点乘的结果。
为什么 x2 不去乘以 y1 呢,因为他们相互垂直,相互不构成任何贡献。
向量点乘的实现:
Vector.py:
PYTHON import math
from ._globals import EPSILON
class Vector:
def __init__(self, lst):
self._values = list(lst)
@classmethod
def zero(cls, dim):
"""返回一个dim维的零向量"""
return cls([0] * dim)
def __add__(self, another):
"""向量加法,返回结果向量"""
assert len(self) == len(another), \
"Error in adding. Length of vectors must be same."
return Vector([a + b for a, b in zip(self, another)])
def __sub__(self, another):
"""向量减法,返回结果向量"""
assert len(self) == len(another), \
"Error in subtracting. Length of vectors must be same."
return Vector([a - b for a, b in zip(self, another)])
def norm(self):
"""返回向量的模"""
return math.sqrt(sum(e**2 for e in self))
def normalize(self):
"""返回向量的单位向量"""
if self.norm() < EPSILON:
raise ZeroDivisionError("Normalize error! norm is zero.")
return Vector(self._values) / self.norm()
def dot(self, another):
"""向量点乘,返回结果标量"""
assert len(self) == len(another), \
"Error in dot product. Length of vectors must be same."
return sum(a * b for a, b in zip(self, another))
def __mul__(self, k):
"""返回数量乘法的结果向量:self * k"""
return Vector([k * e for e in self])
def __rmul__(self, k):
"""返回数量乘法的结果向量:k * self"""
return self * k
def __truediv__(self, k):
"""返回数量除法的结果向量:self / k"""
return (1 / k) * self
def __pos__(self):
"""返回向量取正的结果向量"""
return 1 * self
def __neg__(self):
"""返回向量取负的结果向量"""
return -1 * self
def __iter__(self):
"""返回向量的迭代器"""
return self._values.__iter__()
def __getitem__(self, index):
"""取向量的第index个元素"""
return self._values[index]
def __len__(self):
"""返回向量长度(有多少个元素)"""
return len(self._values)
def __repr__(self):
return "Vector({})".format(self._values)
def __str__(self):
return "({})".format(", ".join(str(e) for e in self._values))
|
向量点乘的应用
由
u⋅v=∥u∥⋅∥v∥⋅cosθ
可得
cosθ=∥u∥⋅∥v∥u⋅v
- 如果 θ=90∘,u⋅v=0
- 如果 u⋅v=0,两个向量方向垂直
- 如果 u⋅v>0,两个向量夹角为锐角
- 如果 u⋅v<0,两个向量夹角为钝角
应用于推荐系统

计算投影点的坐标

投影点的距离:
d=∥v∥cosθ=∥uˉ∥u⋅v
投影点的方向:
u^
投影点的坐标:
Pv=d⋅u^
Numpy 的使用
PYTHON import numpy as np
if __name__ == "__main__":
print(np.__version__)
lst = [1, 2, 3]
lst[0] = "Linear Algebra"
print(lst)
vec = np.array([1, 2, 3])
print(vec)
print(np.zeros(5))
print(np.ones(5))
print(np.full(5, 666))
print(vec)
print("size =", vec.size)
print("size =", len(vec))
print(vec[0])
print(vec[-1])
print(vec[0: 2])
print(type(vec[0: 2]))
vec2 = np.array([4, 5, 6])
print("{} + {} = {}".format(vec, vec2, vec + vec2))
print("{} - {} = {}".format(vec, vec2, vec - vec2))
print("{} * {} = {}".format(2, vec, 2 * vec))
print("{} * {} = {}".format(vec, vec2, vec * vec2))
print("{}.dot({}) = {}".format(vec, vec2, vec.dot(vec2)))
print(np.linalg.norm(vec))
print(vec / np.linalg.norm(vec))
print(np.linalg.norm(vec / np.linalg.norm(vec)))
|









Preview: