前言
这篇文章将会介绍文本形式的影评分类,分为“正面”或“负面”。
这是一个二元分类,也是一种重要且广泛适用的机器学习问题。
我们将使用IMDB数据集,其中包含来自 IMDB 的 50000 条影评文本。
IMDB 是一个电影评价网站,类似于国内的豆瓣。
我们将这些影评拆分为训练集(25000 条影评)和测试集(25000 条影评)。训练集和测试集数量相等。
我们将继续上一篇文章一样,使用 Keras high level API
导入相关库
|
|
下载 IMDB 数据集
TensorFlow 中包含 IMDB 数据集。我们已对该数据集进行了预处理,将影评(字词序列)转换为整数序列,其中每个整数表示字典中的一个特定字词。
以下代码会将 IMDB 数据集下载到您的计算机上(如果您已下载该数据集,则会使用缓存副本):
|
如果是首次运行这个代码:
|
参数 num_words=10000 会保留训练数据中出现频次在前 10000 位的字词。为确保数据规模处于可管理的水平,生僻字词将被舍弃。
探索数据
我们花点时间来了解一下数据的格式。
该数据集已经过预处理:每个样本都是一个整数数组,表示影评中的字词。
每个标签都是整数值 0 或 1,其中 0 表示负面影评,1 表示正面影评。
|
|
影评文本已转换为整数,其中每个整数都表示字典中的一个特定字词。
第一条影评如下所示:
|
|
影评的长度可能会有所不同。以下代码显示了第一条和第二条影评中的字词数。
由于神经网络的输入必须具有相同长度,因此我们稍后需要解决此问题。
|
|
将整数转换回字词
在以下代码中,我们将创建一个辅助函数来查询包含整数到字符串映射的字典对象:
|
这里PAD就是padding,填充的意思,这段代码主要的作用是,改造imdb数据库的word_index,将其中的元素向后移3位,设计几个标志位:<PAD>, <START>, <UNK>, <UNUSED>
如果是初次执行此代码,会有以下输出:
|
现在,我们可以使用 decode_review 函数显示第一条影评的文本:
|
|
构建模型
神经网络通过堆叠层创建而成,这需要做出两个架构方面的主要决策:
- 要在模型中使用多少个层?
- 要针对每个层使用多少个隐藏单元?
在本示例中,输入数据由字词-索引数组构成。要预测的标签是 0 或 1。接下来,我们为此问题构建一个模型:
|
keras的神经网络层如下:
|
按顺序堆叠各个层以构建分类器:
- 第一层是
Embedding层。该层会在整数编码的词汇表中查找每个字词-索引的嵌入向量。模型在接受训练时会学习这些向量。这些向量会向输出数组添加一个维度。生成的维度为:(batch, sequence, embedding)。 - 接下来,一个
GlobalAveragePooling1D层通过对序列维度求平均值,针对每个样本返回一个长度固定的输出向量。这样,模型便能够以尽可能简单的方式处理各种长度的输入。 - 该长度固定的输出向量会传入一个全连接 (
Dense) 层(包含 16 个隐藏单元)。 - 最后一层与单个输出节点密集连接。应用
sigmoid激活函数后,结果是介于 0 到 1 之间的浮点值,表示概率或置信水平。
隐藏单元
上述模型在输入和输出之间有两个中间层(也称为“隐藏”层)。输出(单元、节点或神经元)的数量是相应层的表示法空间的维度。换句话说,该数值表示学习内部表示法时网络所允许的自由度。
如果模型具有更多隐藏单元(更高维度的表示空间)和/或更多层,则说明网络可以学习更复杂的表示法。不过,这会使网络耗费更多计算资源,并且可能导致学习不必要的模式(可以优化在训练数据上的表现,但不会优化在测试数据上的表现)。这称为过拟合,我们稍后会加以探讨。
损失函数和优化器
模型在训练时需要一个损失函数和一个优化器。由于这是一个二元分类问题且模型会输出一个概率(应用 S 型激活函数的单个单元层),因此我们将使用 binary_crossentropy 损失函数。
该函数并不是唯一的损失函数,例如,您可以选择 mean_squared_error。但一般来说,binary_crossentropy 更适合处理概率问题,它可测量概率分布之间的“差距”,在本例中则为实际分布和预测之间的“差距”。
稍后,在探索回归问题(比如预测房价)时,我们将了解如何使用另一个称为均方误差的损失函数。
现在,配置模型以使用优化器和损失函数:
|
创建验证集
在训练时,我们需要检查模型处理从未见过的数据的准确率。我们从原始训练数据中分离出 10000 个样本,创建一个验证集。(为什么现在不使用测试集?我们的目标是仅使用训练数据开发和调整模型,然后仅使用一次测试数据评估准确率。)
|
训练模型
用有 512 个样本的小批次训练模型 40 个周期。这将对 x_train 和 y_train 张量中的所有样本进行 40 次迭代。在训练期间,监控模型在验证集的 10000 个样本上的损失和准确率:
|
|
评估模型
我们来看看模型的表现如何。模型会返回两个值:损失(表示误差的数字,越低越好)和准确率。
|
|
使用这种相当简单的方法可实现约 87% 的准确率。如果采用更高级的方法,模型的准确率应该会接近 95%。
创建准确率和损失随时间变化的图
model.fit() 返回一个 History 对象,该对象包含一个字典,其中包括训练期间发生的所有情况:
|
|
一共有 4 个条目:每个条目对应训练和验证期间的一个受监控指标。我们可以使用这些指标绘制训练损失与验证损失图表以进行对比,并绘制训练准确率与验证准确率图表:
|
|
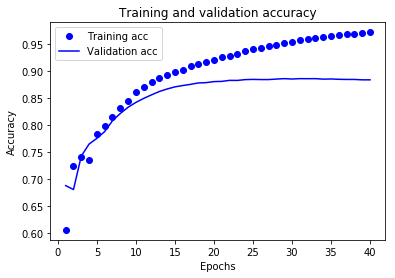
在该图表中,圆点表示训练损失和准确率,实线表示验证损失和准确率。
**训练损失随着周期数的增加而降低,训练准确率随着周期数的增加而提高。**在使用梯度下降法优化模型时,这属于正常现象 - 该方法应在每次迭代时尽可能降低目标值。
验证损失和准确率的变化情况并非如此,它们似乎在大约 20 个周期后达到峰值。这是一种过拟合现象:模型在训练数据上的表现要优于在从未见过的数据上的表现。在此之后,模型会过度优化和学习特定于训练数据的表示法,而无法泛化到测试数据。
对于这种特殊情况,我们可以在大约 20 个周期后停止训练,防止出现过拟合。




Preview: