机器学习tensorflow-keras之预测汽车燃油效率-回归问题

前言

回归问题的目标是预测一系列连续值的输出，比如价格和概率。和分类问题不一样，分类问题是从一堆中选出一类。（比方说从一堆照片中选出带有苹果的照片等）

这篇文章使用 Auto MPG 数据集来构建模型，预测上世纪70年到80年代的汽车燃油效率。这些数据包含：气缸、排量、马力和重量等属性。

我们需要使用seaborn来绘制一些图像：

 SHELL$ pip install seaborn

首次运行上述代码时：

 CONSOLECollecting seaborn
  Downloading https://files.pythonhosted.org/packages/a8/76/220ba4420459d9c4c9c9587c6ce607bf56c25b3d3d2de62056efe482dadc/seaborn-0.9.0-py3-none-any.whl (208kB)
    100% |################################| 215kB 10kB/s
Requirement already satisfied: scipy>=0.14.0 in /usr/local/lib/python3.5/dist-packages (from seaborn) (1.1.0)
......
Installing collected packages: seaborn
Successfully installed seaborn-0.9.0

引入此项目使用的依赖库

 PYTHONfrom __future__ import absolute_import, division, print_function

import pathlib

import pandas as pd
import seaborn as sns

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers

print(tf.__version__)

输出tensorflow版本如下：

 CONSOLE1.12.0

Auto MPG 数据集

数据集来自UCI Machine Learning Repository

MPG 意为 Miles per Gallon，衡量一辆汽车在你的油箱中只加一加仑汽油或柴油可以行驶多少英里。

获取数据

首先，使用keras下载数据

 PYTHONdataset_path = keras.utils.get_file("auto-mpg.data", "https://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")
dataset_path

输出auto-mpg.data文件存放地址：

 CONSOLEDownloading data from https://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data
32768/30286 [================================] - 0s 1us/step

'/root/.keras/datasets/auto-mpg.data'

使用pandas引入数据集

 PYTHONcolumn_names = ['MPG','Cylinders','Displacement','Horsepower','Weight',
                'Acceleration', 'Model Year', 'Origin'] 
raw_dataset = pd.read_csv(dataset_path, names=column_names,
                      na_values = "?", comment='\t',
                      sep=" ", skipinitialspace=True)

dataset = raw_dataset.copy()
dataset.tail()

na_values = "?"：na 意为 not available，即不可用。

dataset.tail()输出最后5行，你也可以执行dataset.tail(10)来输出10行或自定义一个数字，来观察表格数据。

	MPG	Cylinders	Displacement	Horsepower	Weight	Acceleration	Model Year	Origin
393	27.0	4	140.0	86.0	2790.0	15.6	82	1
394	44.0	4	97.0	52.0	2130.0	24.6	82	2
395	32.0	4	135.0	84.0	2295.0	11.6	82	1
396	28.0	4	120.0	79.0	2625.0	18.6	82	1
397	31.0	4	119.0	82.0	2720.0	19.4	82	1

经过pands处理，?变成了NaN

清洗数据

数据集某些行有几个?的值

使用pandas来统计一下这些值的数量：

 PYTHONdataset.isna().sum()

其中isna()意为is not available

 CONSOLEMPG             0
Cylinders       0
Displacement    0
Horsepower      6
Weight          0
Acceleration    0
Model Year      0
Origin          0
dtype: int64

为了简单起见，我们删除这些数据不完整的行：

 PYTHONdataset = dataset.dropna()

Origin列代表汽车的产地，1代表美国，2代表欧洲，3代表日本，为了学习方便，我们把它转化为相应的列，是为1，不是为0

首先，删除Origin列，将它存到变量origin里

 PYTHONorigin = dataset.pop('Origin')

然后，进项判断，添加到新的列里面去

 PYTHONdataset['USA'] = (origin == 1)*1.0
dataset['Europe'] = (origin == 2)*1.0
dataset['Japan'] = (origin == 3)*1.0
dataset.tail()

注意：True==1.000000000000001（小数点后15位）的结果是False，True==1.0000000000000001（小数点后16位）的结果是True

	MPG	Cylinders	Displacement	Horsepower	Weight	Acceleration	Model Year	USA	Europe	Japan
393	27.0	4	140.0	86.0	2790.0	15.6	82	1.0	0.0	0.0
394	44.0	4	97.0	52.0	2130.0	24.6	82	0.0	1.0	0.0
395	32.0	4	135.0	84.0	2295.0	11.6	82	1.0	0.0	0.0
396	28.0	4	120.0	79.0	2625.0	18.6	82	1.0	0.0	0.0
397	31.0	4	119.0	82.0	2720.0	19.4	82	1.0	0.0	0.0

分割数据集

把数据集分割为训练集和测试集。

测试集在最后验证评估的时候使用。

 PYTHONtrain_dataset = dataset.sample(frac=0.8,random_state=0)
test_dataset = dataset.drop(train_dataset.index)

frac=0.8 Fraction 代表80%，如果是n=320，代表320个。ps: n和frac不可同时使用

random_state随机数生成器的种子数

观察数据

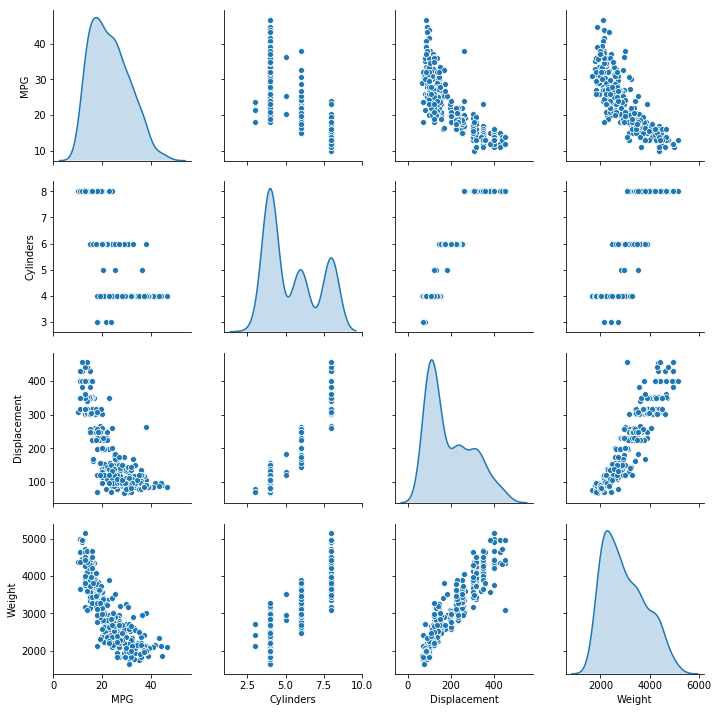
使用seaborn观察数据分布情况

关于sns.pairplot的文档请参阅https://seaborn.pydata.org/generated/seaborn.pairplot.html

 PYTHONsns.pairplot(train_dataset[["MPG", "Cylinders", "Displacement", "Weight"]], diag_kind="kde")

seaborn生成的图片

再看看数据统计：

 PYTHONtrain_stats = train_dataset.describe()
train_stats.pop("MPG")
train_stats = train_stats.transpose()
train_stats

	count	mean	std	min	25%	50%	75%	max
Cylinders	314.0	5.477707	1.699788	3.0	4.00	4.0	8.00	8.0
Displacement	314.0	195.318471	104.331589	68.0	105.50	151.0	265.75	455.0
Horsepower	314.0	104.869427	38.096214	46.0	76.25	94.5	128.00	225.0
Weight	314.0	2990.251592	843.898596	1649.0	2256.50	2822.5	3608.00	5140.0
Acceleration	314.0	15.559236	2.789230	8.0	13.80	15.5	17.20	24.8
Model Year	314.0	75.898089	3.675642	70.0	73.00	76.0	79.00	82.0
USA	314.0	0.624204	0.485101	0.0	0.00	1.0	1.00	1.0
Europe	314.0	0.178344	0.383413	0.0	0.00	0.0	0.00	1.0
Japan	314.0	0.197452	0.398712	0.0	0.00	0.0	0.00	1.0

其中count 代表总数量，mean代表均值，std代表标准差 (standard deviation)，min代表最小值，max代表最大值

25%代表一分位数(一分位数：1/4，二分位数：2/4，以此类推)。

以排量举例，上表Displacement中：25%的汽车小于105.5的排量，50%的汽车小于151.0的排量，75%的汽车小于265.75的排量，以此类推

从数据集中提取MPG值

MPG值是我们训练模型来预测的值，所以要将其从数据集中提取出来作为labels

 PYTHONtrain_labels = train_dataset.pop('MPG')
test_labels = test_dataset.pop('MPG')

标准化数据

从train_stats表格里面的数据，我们可以看出数据特征范围的差异性有多大。

标准分数（Standard Score，又称z-score，中文称为Z-分数或标准化值）^[1]

$z = {x-\mu\over 2\sigma}.​$

• $x​$ 是需要被标准化的原始分数
• $\mu$ 是母体的平均值
• $\sigma​$ 是母体的标准差

如果数据太过随机，没有特征或特征不规律，会使得训练变难，使训练结果过度依赖原始数据的随机特征。

尽管train_stats是从训练集中统计的，但还是可以重复利用之

 PYTHONdef norm(x):
  return (x - train_stats['mean']) / train_stats['std']

normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)

再次观察

让我们再来看看标准化处理过的数据长什么样子：

 PYTHONnormed_train_data.describe().transpose()

	count	mean	std	min	25%	50%	75%	max
Cylinders	314.0	1.824443e-16	1.0	-1.457657	-0.869348	-0.869348	1.483887	1.483887
Displacement	314.0	8.627211e-17	1.0	-1.220325	-0.860894	-0.424785	0.675074	2.489002
Horsepower	314.0	-9.900078e-18	1.0	-1.545283	-0.751241	-0.272190	0.607162	3.153347
Weight	314.0	-8.485781e-17	1.0	-1.589352	-0.869478	-0.198782	0.732017	2.547401
Acceleration	314.0	-5.148041e-16	1.0	-2.710152	-0.630725	-0.021237	0.588250	3.313017
Model Year	314.0	9.772791e-16	1.0	-1.604642	-0.788458	0.027726	0.843910	1.660094
USA	314.0	7.920062e-17	1.0	-1.286751	-1.286751	0.774676	0.774676	0.774676
Europe	314.0	1.980016e-17	1.0	-0.465148	-0.465148	-0.465148	-0.465148	2.143005
Japan	314.0	5.374328e-17	1.0	-0.495225	-0.495225	-0.495225	-0.495225	2.012852

可以明显看到，数据均值为0，标准差为1^[2]

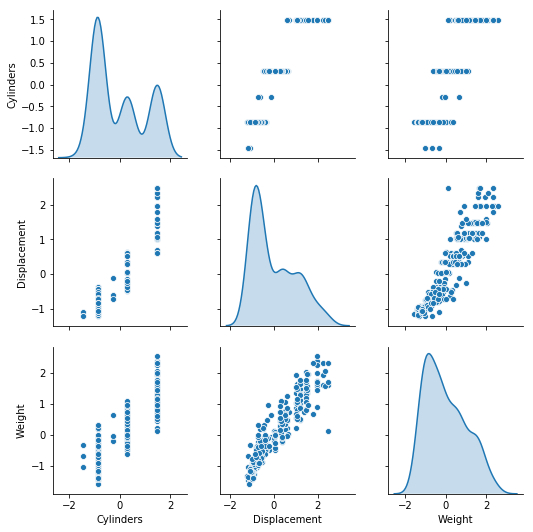
使用seaborn观察经过标准化处理的数据分布情况：

 PYTHONsns.pairplot(normed_train_data[["Cylinders", "Displacement", "Weight"]], diag_kind="kde")

数据有规律了许多

模型

构建模型

我们使用Sequential模型，添加两个全连接的Dense layers，一个大小为1的Dense layer，作为预测结果。

并用函数build_model包裹起来，因为后文我们还要再创建一个模型。

 PYTHONdef build_model():
  model = keras.Sequential([
    layers.Dense(64, activation=tf.nn.relu, input_shape=[len(train_dataset.keys())]),
    layers.Dense(64, activation=tf.nn.relu),
    layers.Dense(1)
  ])

  optimizer = tf.keras.optimizers.RMSprop(0.001)

  model.compile(loss='mse',
                optimizer=optimizer,
                metrics=['mae', 'mse'])
  return model

 PYTHONmodel = build_model()

查看模型

使用summary()方法，打印简单的模型信息

 PYTHONmodel.summary()

 CONSOLE_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense (Dense)                (None, 64)                640       
_________________________________________________________________
dense_1 (Dense)              (None, 64)                4160      
_________________________________________________________________
dense_2 (Dense)              (None, 1)                 65        
=================================================================
Total params: 4,865
Trainable params: 4,865
Non-trainable params: 0
_________________________________________________________________

现在，取前10个样本来做预测尝试看看程序是否能正确运行：

 PYTHONexample_batch = normed_train_data[:10]
example_result = model.predict(example_batch)
example_result

 CONSOLEarray([[-0.00998245],
       [ 0.04613847],
       [-0.00575289],
       [ 0.13950706],
       [ 0.5010514 ],
       [ 0.01313432],
       [ 0.5347774 ],
       [ 0.32584202],
       [ 0.0665579 ],
       [ 0.4367365 ]], dtype=float32)

虽然值不正确，但产生了期待的数据类型，说明我们的模型的对的。

训练模型

训练1000批次，同时记录下训练和验证的准确率。

 PYTHON# Display training progress by printing a single dot for each completed epoch
class PrintDot(keras.callbacks.Callback):
  def on_epoch_end(self, epoch, logs):
    if epoch % 100 == 0: print('')
    print('.', end='')

EPOCHS = 1000

history = model.fit(
  normed_train_data, train_labels,
  epochs=EPOCHS, validation_split = 0.2, verbose=0,
  callbacks=[PrintDot()])

 CONSOLE....................................................................................................
.............................................................................
more output omitted
....................................................................................................

利用pandas把训练记录可视化：

 PYTHONhist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()

	loss	mean_absolute_error	mean_squared_error	val_loss	val_mean_absolute_error	val_mean_squared_error	epoch
995	2.838588	1.055799	2.838588	9.635040	2.360446	9.635040	995
996	2.627797	1.077834	2.627797	10.011816	2.454931	10.011816	996
997	2.791595	1.062792	2.791595	9.421341	2.350526	9.421341	997
998	2.828236	1.110399	2.828236	9.730920	2.364439	9.730920	998
999	2.727029	1.034335	2.727029	9.779824	2.373134	9.779824	999

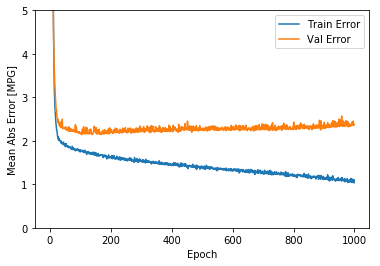
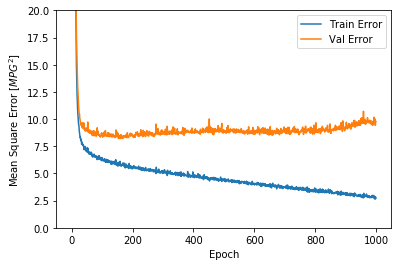
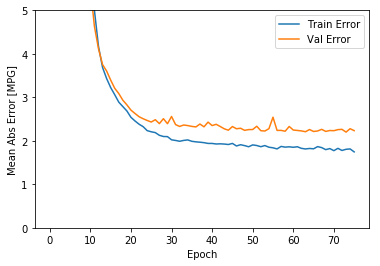
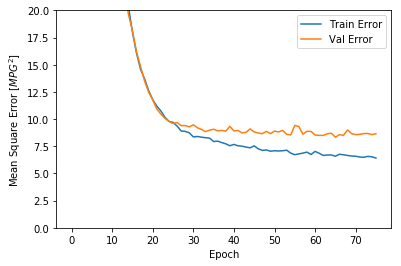
 PYTHONimport matplotlib.pyplot as plt

def plot_history(history):
  hist = pd.DataFrame(history.history)
  hist['epoch'] = history.epoch
  
  plt.figure()
  plt.xlabel('Epoch')
  plt.ylabel('Mean Abs Error [MPG]')
  plt.plot(hist['epoch'], hist['mean_absolute_error'],
           label='Train Error')
  plt.plot(hist['epoch'], hist['val_mean_absolute_error'],
           label = 'Val Error')
  plt.legend()
  plt.ylim([0,5])
  
  plt.figure()
  plt.xlabel('Epoch')
  plt.ylabel('Mean Square Error [$MPG^2$]')
  plt.plot(hist['epoch'], hist['mean_squared_error'],
           label='Train Error')
  plt.plot(hist['epoch'], hist['val_mean_squared_error'],
           label = 'Val Error')
  plt.legend()
  plt.ylim([0,20])

plot_history(history)

这两张图表明，在大概100多个批次之后，错误率降低的太少了，甚至验证错误率还稍稍上升了一些。

我们需要在适当的时候使用EarlyStopping回调函数来测试每个批次的训练条件，如果经过一定数量的批次，还没有改进，则自动停止训练。

您可以在此处了解有关此回调的更多信息。

 PYTHONmodel = build_model()

# The patience parameter is the amount of epochs to check for improvement
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)

history = model.fit(normed_train_data, train_labels, epochs=EPOCHS,
                    validation_split = 0.2, verbose=0, callbacks=[early_stop, PrintDot()])

plot_history(history)

 CONSOLE............................................................................

现在，大概验证的错误率是 $\pm2 $ 多一点。

我们使用它来进行预测吧。测试集没有参与训练，测试集的测试结果将会向我们展示训练的模型在实际中效果如何。

 PYTHONloss, mae, mse = model.evaluate(normed_test_data, test_labels, verbose=0)
print("Testing set Mean Abs Error: {:5.2f} MPG".format(mae))

 CONSOLETesting set Mean Abs Error:  1.84 MPG

做出预测

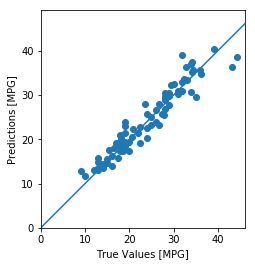
 PYTHONtest_predictions = model.predict(normed_test_data).flatten()

plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
plt.axis('equal')
plt.axis('square')
plt.xlim([0,plt.xlim()[1]])
plt.ylim([0,plt.ylim()[1]])
_ = plt.plot([-100, 100], [-100, 100])

这张图x坐标代表实际值，y坐标代表预测值，所以当点越集中在中间那条反对角线的时候，说明预测越准。

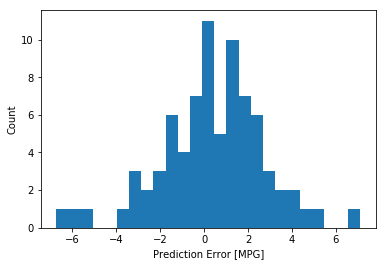
看看错误的分布情况

 PYTHONerror = test_predictions - test_labels
plt.hist(error, bins = 25)
plt.xlabel("Prediction Error [MPG]")
_ = plt.ylabel("Count")

有点正态分布的意思，但是不严格，因为数据量确实太少了。

结论

• 均方误差（MSE）是用于回归问题的常见损失函数。
• 用于回归的评估指标，常见的回归度量是平均绝对误差（MAE）。
• 当数字输入数据要素具有不同范围的值时，应将每个特征独立地缩放到相同范围。
• 如果没有太多的训练数据，创建一个隐藏层少的小网络，以避免过度拟合。
• 早期停止是防止过拟合的有用技术。

代码

你可以在这里：https://github.com/HarborZeng/fuel_efficiency找到和本文一样的Jupyter Notebook^[3]代码，进行学习。更多Jupyter Notebook的用法，请参考：https://jupyter.org/

参考资料

---

1. 标准分数 https://zh.wikipedia.org/wiki/標準分數 ↩︎

2. 再谈机器学习中的归一化方法（Normalization Method）https://blog.csdn.net/zbc1090549839/article/details/44103801 ↩︎

3. Project Jupyter https://jupyter.org/ ↩︎