线性代数第二章：一切从向量开始

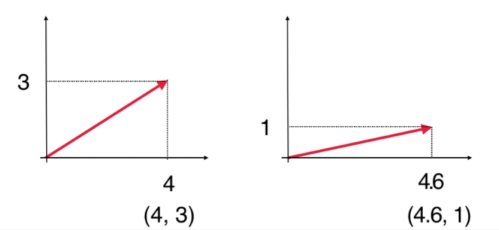
什么是向量

• 为什么线性代数很重要？线性代数使数学的研究从一个数扩展到一组数。

• 一组数就是向量（Vector）

• 研究一组数有什么用？最基本的出发点：表示方向。假如说 5km，我们不知道往哪个方向去的 5km，在二维平面中，至少需要两个数，才能确定方向，

• 向量是线性代数研究的基本元素

• 向量的起始点不重要，为方便起见，全部看做从原点出发

• 向量的顺序重要，不同的顺序是不同的向量

• 向量可以描述 $n$ 纬的世界，不仅仅是平面或 3 维空间

  比如刻画一个房子：

  面积	卧室	卫生间	最近地铁站	价格
  120	3	2	2	666

  可用 $(120,3,2,2,666)$ 来描述此房子，看似不表示方向，但却是高维空间中的点，在高维空间中表示方向，只是我们没办法直观理解高维空间中的点。

• 向量不仅仅是一组数，更是一个有向线段，更是空间中的一个点

向量的更多属于和表示法

向量更严格的定义：

• 一个数字是标量，一组数字是向量
• 向量上面画箭头或粗体，如：$\vec \lambda$、$\boldsymbol \lambda$，标量仅用代数，用符号代表数
• 行向量：$(3,4)$、列向量：$\begin{pmatrix}3\\4\end{pmatrix}$，使用中更常见的把数字码成一列，也可以使用 $(3,4)^T$ 转置用行向量的方式表示列向量

实现自己的向量

在 python 中，我们使用数组来保存向量中的数字。

class Vector:

    def __init__(self, lst):
        self._values = lst

    def __getitem__(self, index):
        """取向量的第index个元素"""
        return self._values[index]

    def __len__(self):
        """返回向量长度（有多少个元素）"""
        return len(self._values)

    def __repr__(self):
        return "Vector({})".format(self._values)

    def __str__(self):
        return "({})".format(", ".join(str(e) for e in self._values))

向量的基本运算

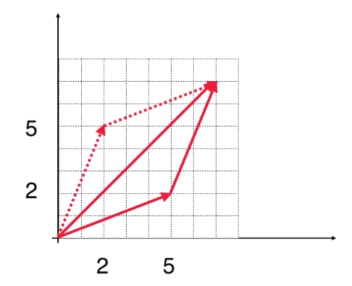
向量加法

如 $(5,2)^T+(2,5)^T=(7,7)^T$

向量相加等于两个向量首尾相接构成的平行四边形的对角线。

数量乘法

如 $2\times (5,2)^T=(10,4)^T$

数量相乘相当于 2 个 $(5,2)$ 相加。

推广到 $n$ 纬中：

$k \cdot \begin{pmatrix} v_1\\v_2\\\dots\\v_n \end{pmatrix}= \begin{pmatrix} k\cdot v_1\\k\cdot v_2\\\dots\\k\cdot v_n \end{pmatrix}$

实现向量的基本运算

class Vector:

    def __init__(self, lst):
        self._values = list(lst)

    def __add__(self, another):
        """向量加法，返回结果向量"""
        assert len(self) == len(another), \
            "Error in adding. Length of vectors must be same."

        # return Vector([a + b for a, b in zip(self._values, another._values)])
        return Vector([a + b for a, b in zip(self, another)])

    def __sub__(self, another):
        """向量减法，返回结果向量"""
        assert len(self) == len(another), \
            "Error in subtracting. Length of vectors must be same."

        return Vector([a - b for a, b in zip(self, another)])

    def __mul__(self, k):
        """返回数量乘法的结果向量：self * k"""
        return Vector([k * e for e in self])

    def __rmul__(self, k):
        """返回数量乘法的结果向量：k * self"""
        return self * k

    def __pos__(self):
        """返回向量取正的结果向量"""
        return 1 * self

    def __neg__(self):
        """返回向量取负的结果向量"""
        return -1 * self

    def __iter__(self):
        """返回向量的迭代器"""
        return self._values.__iter__()

    def __getitem__(self, index):
        """取向量的第index个元素"""
        return self._values[index]

    def __len__(self):
        """返回向量长度（有多少个元素）"""
        return len(self._values)

    def __repr__(self):
        return "Vector({})".format(self._values)

    def __str__(self):
        return "({})".format(", ".join(str(e) for e in self._values))

向量基本运算的性质

• 交换律1：$\vec u + \vec v = \vec v + \vec u$
• 交换律2：$(\vec u + \vec v) + \vec w = \vec v + (\vec u + \vec w)$
• 结合律1：$k(\vec u + \vec v)=k\vec u+k\vec v$
• 结合律2：$(k+c)\vec u=k\vec u+c\vec u$
• 交换律3：$(kc)\vec u=k(c\vec{u})$
• $1\vec{u}=\vec{u}$

举例证明：$k(\vec u + \vec v)=k\vec u+k\vec v$

$k(\vec{u}+\vec{v})=k\left(\begin{array}{c} u_{1} \\ u_{2} \\ \cdots \\ u_{n} \end{array}\right)+\left(\begin{array}{c} v_{1} \\ v_{2} \\ \cdots \\ v_{n} \end{array}\right)=k\left(\begin{array}{c} u_{1}+v_{1} \\ u_{2}+v_{2} \\ \cdots \\ u_{n}+v_{n} \end{array}\right)=\left(\begin{array}{c} k u_{1}+k v_{1} \\ k u_{2}+k v_{2} \\ \cdots \\ k u_{n}+k v_{n} \end{array}\right)$

$k \vec{u}+k \vec{v}=k\left(\begin{array}{c} u_{1} \\ u_{2} \\ \cdots \\ u_{n} \end{array}\right)+k\left(\begin{array}{c} v_{1} \\ v_{2} \\ \cdots \\ v_{n} \end{array}\right)=\left(\begin{array}{c} k u_{1} \\ k u_{2} \\ \cdots \\ k u_{n} \end{array}\right)+\left(\begin{array}{c} k v_{1} \\ k v_{2} \\ \cdots \\ k v_{n} \end{array}\right)=\left(\begin{array}{c} k u_{1}+k v_{1} \\ k u_{2}+k v_{2} \\ \cdots \\ k u_{n}+k v_{n} \end{array}\right)$

左边等于右边，证明完毕。

零向量

零向量：对于任意一个向量 $\vec u$，都存在一个向量 $\boldsymbol O$ ，满足 $\vec{u}+\boldsymbol{O}=\vec{u}$。

证明：

因为

$\vec{u}+O=\left(\begin{array}{c} u_{1} \\ u_{2} \\ \ldots \\ u_{n} \end{array}\right)+\left(\begin{array}{c} o_{1} \\ o_{2} \\ \ldots \\ o_{n} \end{array}\right)=\left(\begin{array}{c} u_{1}+o_{1} \\ u_{2}+o_{2} \\ \ldots \\ u_{n}+o_{n} \end{array}\right)=\left(\begin{array}{c} u_{1} \\ u_{2} \\ \ldots \\ u_{n} \end{array}\right)$

所以

$\left\{\begin{array}{c} u_{1}+o_{1}=u_{1} \\ u_{2}+o_{2}=u_{2} \\ \ldots \\ u_{n}+o_{n}=u_{n} \end{array} \Rightarrow\left\{\begin{array}{c} o_{1}=0 \\ o_{2}=0 \\ \ldots \\ o_{n}=0 \end{array} \Rightarrow O=\left(\begin{array}{c} 0 \\ 0 \\ \ldots \\ 0 \end{array}\right)\right.\right.$

注意：零向量不用箭头，零向量没有长度（不用定义有几个0）。

可以从零向量引申出负向量：对于任意一个向量 $\vec u$，都存在一个向量 $\vec{-u}$ ，满足 $\vec{u}+\vec{-u}=\boldsymbol{O}$，且上述 $\vec{-u}$ 唯一。此定理可用反证法证明。

代码实现零向量（在 class Vector 里添加）：

@classmethod
def zero(cls, dim):
    """返回一个dim维的零向量"""
    return cls([0] * dim)